Mass per unit area of disc \(= \frac{M}{{\pi {R^2}}}\)
Mass of removed portion of disc,
\(M' = \frac{M}{{\pi {R^2}}} \times \pi {\left( {\frac{R}{2}} \right)^2} = \frac{M}{4}\)
Moment of inertia of removed portion about an axis passing through center of disc \(O\) and perpendicular to the plane od disc,
\(I{'_0} = {I_0} + M'{d^2}\)
\(= \frac{1}{2} \times \frac{M}{4} \times {\left( {\frac{R}{2}} \right)^2} + \frac{M}{4} \times {\left( {\frac{R}{2}} \right)^2}\)
\(= \frac{{M{R^2}}}{{32}} + \frac{{M{R^2}}}{{16}} = \frac{{3M{R^2}}}{{32}}\)
When portion of disc would not have been removed, the moment of inertia of complete disc about center \(O\) is
\({I_0} = \frac{1}{2}M{R^2}\)
So, moment of inertia of the disc with removed portion is
\(I = {I_0} - {I_0} = \frac{1}{2}M{R^2} - \frac{{3M{R^2}}}{{32}} = \frac{{13M{R^2}}}{{32}}\)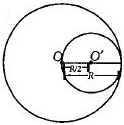
Download our appand get started for free
Similar Questions
- 1$M$ દળ અને $r$ ત્રિજ્યાની પાતળી તકતી તેની અક્ષને અનુલક્ષીને $\omega_1$ કોણીય ઝડપથી ભ્રમણ કરે છે, જો વ્યાસના બિંદુએ $m$ દળના બે નાના ગોળા મૂકવામાં આવે, તો તેની અંતિમ કોણીય ઝડપ કેટલી થશે?View Solution
- 2$M $ દળ અને $R$ ત્રિજ્યાવાળો નક્કર નળાકાર $ L$ લંબાઈના ઢાળ પરથી સરક્યા સિવાય ગબડે છે. ઢાળની ઊચાઈ $h$ છે. જ્યારે નળાકાર ઢાળના તળિયે પહોંચે ત્યારે તેના દ્રવ્યમાન-કેન્દ્રનો વેગ કેટલો હશે ?View Solution
- 3$2\ kg$ દળ અને $ 0.2\ m$ ત્રિજ્યાનો ઘન નળાકાર $3\ rad/sec$ ના કોણીય વેગથી ચાકગતિ કરે છે $0.5\ kg$ દળનો કણ $5\ ms^{-1} $ ના વેગથી ગતિ કરતા તેના પરિઘ પર અથડાય છે અને ચોટી જાય છે તો અથડામણના લીધે ગતિઊર્જામાં ....... $J$ ઊર્જાનો વ્યય થાય છે.View Solution
- 4એ કારનું પૈડું $1200\ r.p.m.$ ની ઝડપથી ફરે છે $10\ sec$ માટે પ્રવેગ આપતા તે $4500\ r.p.m. $ ની ઝડપે ફરવા લાગે તો પૈડાંનો કોણીય પ્રવેગ કેટલો થાય ?View Solution
- 5$L$ લંબાઈ અને $ M$ દળના પાતળા સળિયાના એક છેડાથી $ L/3$ અંતરે રહેલાં બિંદુમાંથી પસાર થતી અને સળિયાને લંબ અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 6સ્થાનસદિશ $\mathop {{r_1}}\limits^ \to \,\, = \,\,\hat i\,\, + \,\,2\hat j\,\, + \,\,3\hat k$ ધરાવતા બિંદુ આગળ બળ $\mathop F\limits^ \to \,\, = \,\,4\hat i\,\, - \,\,5\hat j\,\, + \,\,3\hat k$ લગાડવામાં આવે છે. $\mathop {{r_2}}\limits^ \to \,\, = \,\,3\hat i\,\, - \,\,2\hat j\,\, - \,\,3\hat k$ સ્થાનસદિશ ધરાવતા બિંદુએ લાગતું ટૉર્ક .......View Solution
- 7$1\ kg$ નો એક પદાર્થ $2\ ms^{-1}$ જેટલા રેખીય વેગથ ધન $X -$ અક્ષને સમાંતર ગતિ કરી રહ્યો છે. આ ગતિ દરમિયાન ઉગમબિંદુથી તેનું લઘુતમ અંતર $ 12\ cm $ થાય છે, તો આ પદાર્થનું ઉગમબિંદુને અનુલક્ષીને કોણીય વેગમાન ....... $Js$View Solution
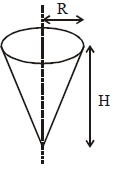
- 8આકૃતિમાં પોલો આઇસ્ક્રીમ કોન છે ,તેનું દળ $M,$ ઉપરની ત્રિજ્યા $R$ અને ઊંચાઈ $H$ છે,તો આપેલી અક્ષને અનુલક્ષીને જડત્વની ચાક્માત્રા ......View Solution
- 9પ્રત્યેકનું દળ $2 \mathrm{M}$ હોય તેવા એક સરખા ગોળાઓને $4 \mathrm{~m}$ લંબાઈ ધરાવતી પરસ્પર લંબ બાજુઓ વાળા કાટકોણ ત્રિકોણનાશિરોબિંદુુઓ પર મૂકેલાછે. આ બે બાજુઓના છેદબિંદુને ઉગમબિંદુ તરીકે લેતા તંત્રના દ્રવ્યમાન કેન્દ્રના સ્થાન સદિશનું મૂલ્ય$\frac{4 \sqrt{2}}{x}$ છે, જયા $x$ મૂલ્ય___________છે.View Solution
- 10$L$ લંબાઇનો સળિયા બે માણસના ખંભા પર છે. છેડા પરના એક માણસ પર $ 1\over 4 $ માં ભાગનું વજનબળ લાગે છે. તો બીજો માણસ આ છેડાથી કેટલે દૂર હશે?View Solution
