Excess electrons on an oil drop, \(n=12\)
Electric field intensity, \(E =2.55 \times 10^{4} \,N \,C ^{-1}\)
Density of oil, \(\rho=1.26 \,gm / cm ^{3}=1.26 \times 10^{3} \,kg / m ^{3}\)
Acceleration due to gravity, \(g=9.81 \,m\, s ^{-2}\)
Charge on an electron, \(e=1.6 \times 10^{-19} \,C\)
Radius of the oil drop \(= r\)
Force \((F)\) due to electric field \(E\) is equal to the weight of the oil drop \((W)\)
\(F = W \Rightarrow E q=m g \Rightarrow\) \(Ene\) \(=\frac{4}{3} \pi r^{3} \times \rho \times g\)
Where, \(q =\) Net charge on the oil drop \(= ne\) \(m =\) Mass of the oil drop \(=\) Volume of the drop \(\times\) Density of oil \(=\frac{4}{3} \pi r^{3} \times \rho\)
\(r=\left[\frac{3 E n e}{4 \pi \rho g}\right]^{\frac{1}{3}}=\left[\frac{3 \times 2.55 \times 10^{4} \times 12 \times 1.6 \times 10^{-19}}{4 \times 3.14 \times 1.26 \times 10^{3} \times 9.81}\right]^{\frac{1}{3}}\)
\(=\left[946.09 \times 10^{-21}\right]^{\frac{1}{3}}=9.82 \times 10^{-7} \,mm\)
Therefore, the radius of the oil drop is \(9.82 \times 10^{-4} \;mm\).
Download our appand get started for free
Similar Questions
- 1એક વિદ્યુતભાર $Q$ બે ભાગ $Q_1$ અને $Q_2$ માં વહેચાય છે. આ વિદ્યુતભારો $R$ અંતરે મૂકેલા છે. તેઓ વચ્ચેનું મહત્તમ અપાકર્ષી બળ માટે $Q_1$ અને $Q_2$ શું હશે ?View Solution
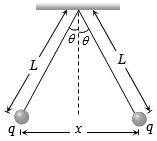
- 2$m$ દળ ધરાવતા અને $q$ વિદ્યુતભાર ધરાવતા બે ગોળાને આકૃતિ મુજબ બાંધેલા છે.જો ખૂણો $\theta$ સૂક્ષ્મ હોય,તો $X$ = _____View Solution
- 3એક $p$ ડાયપોલ મોમેન્ટ ધરાવતા ડાયપોલના લંબ દ્વિભાજક પર બિંદુ $Q$ છે. જો બિંદુ $Q$ નું ડાયપોલથી અંતર $r$ (ડાયપોલની સાઇઝ કરતાં ઘણું મોટું) હોય તો, $Q$ પર વિદ્યુતક્ષેત્ર કોના સપ્રમાણમા હોય?View Solution
- 4$q$ વિદ્યુતભાર સાથે $r\, (r < R)$ ના વિદ્યુતભારીત ગોળીય વાહકના કેન્દ્રથી $r$ (અંતરે $R$) આવેલા બિંદુ આગળ વિદ્યુતક્ષેત્રની તીવ્રતા ....... હશે.View Solution
- 5આકૃતિમાં બતાવ્યા પ્રમાણે $L$ લંબાઈના અને $Q$ વિદ્યુતભાર વાળા પાતળા અવાહક સળિયા (તેની લંબાઈ પર સમાન વિતરણ થયેલ છે.) ના એક છેડાથી અંતરે એક બિંદુવત વિદ્યુતભાર મૂકેલો છે. તે બંને વચ્ચેના વિદ્યુતબળનું મૂલ્ય શોધો.View Solution
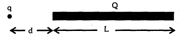
- 6બે બિંદુગત વિદ્યુતભારો $e$ અને $3 e$ ને $r$ અંતરે મૂકવામાં આવ્યા છે. વિદ્યુતભારથી કેટલા અંતરે વિદ્યુતક્ષેત્ર તીવ્રતા શૂન્ય હશે ?View Solution
- 7જ્યારે ધાતુના તટસ્થ ગોળામાંથી $10^{14}$ ઈલેકટ્રોનસને દૂર કરવામાં આવે તો ગોળા પરનો વિદ્યુતભાર.......$\mu C$ હશે ?View Solution
- 8મુક્ત અવકાશમાં $z-$અક્ષ પર $8\, nC / m$ ના સમાંગ રેખીય વિદ્યુતભાર ધરાવતાં વિસ્તરમાં $x =3\, m$ બિંદુ આગળ વિદ્યુત ફલક્સ ઘનતા શોધો :View Solution
- 9View Solutionસમાંગ વિદ્યુતક્ષેત્રમાં મૂકેલ વિદ્યુત ડાયપોલ કઈ સ્થિતિમાં બળયુગ્મની મહત્તમ ચાકમાત્રા અનુભવે છે ?
- 10બે બિંદુવત વિદ્યુતભારો $q_1$ અને $q_2$ હવામાં એકબીજાથી $50\, cm$ અંતરે આવેલા છે. અને અમુક ચોકકસ બળથી આંતરક્રિયા કરે છે હવે સમાન વિદ્યુતભારો જેની સાપેક્ષ પરિમિટિવિટિ $5$ હોય તેવા તેલમાં મૂકવામાં આવે છે. જો તેમના વચ્ચેનું આંતર બળ સમાન હોય તો તેલમાં અંતર ........ $cm$ છે.View Solution
