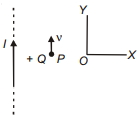
$N$ આંટા ધરાવતી સ્પાયરલ કોઇલની અંદરની ત્રિજયા $a$ અને બહારની ત્રિજયા $b$ છે. તેમાંથી $I$ પ્રવાહ પસાર કરતાં કેન્દ્ર આગળ ચુંબકીયક્ષેત્ર કેટલું થાય?
IIT 2001, Diffcult
c
(c) Number of turns per unit width \( = \frac{N}{{b - a}}\)
(c) Number of turns per unit width \( = \frac{N}{{b - a}}\)
Consider an elemental ring of radius \(x\) and with thickness \(dx\)
Number of turns in the ring \( = dN = \frac{{Ndx}}{{b - a}}\)
Magnetic field at the centre due to the ring element \(dB = \frac{{{\mu _0}(dN)i}}{{2x}} = \frac{{{\mu _0}i}}{2}.\frac{{Ndx}}{{(b - a)}}.\frac{1}{x}\)
\(\therefore \) Field at the centre \( = \int_{}^{} {dB = \frac{{{\mu _0}Ni}}{{2(b - a)}}} \int_a^b {\frac{{dx}}{x}} \) \( = \frac{{{\mu _0}Ni}}{{2(b - a)}}\ln \frac{b}{a}.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1અર્ધઆવર્તન પ્રક્રિયાનો ઉપયોગ કરીને ગેલ્વેનોમીટરનો અવરોધ $G$ શોધવાના પરિપથમાં $V_E\;emf$ ની બેટરી અને $R\;\Omega $ ના અવરોધનો ઉપયોગ કરતાં ગેલ્વેનોમીટર $\theta $ જેટલા ખૂણાનું આવર્તન દર્શાવે છે. જો ગેલ્વેનોમીટરનું અર્ધઆવર્તન દર્શાવવા $S$ જેટલા શંટ અવરોધની જરૂર પડતી હોય તો $G, R$ અને $S$ વચ્ચેનો સંબંધ કયા સમીકરણ દ્વારા આપી શકાય?View Solution
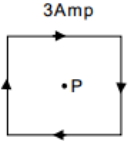
- 2$20$ સેમી બાજુવાળા ચોરસના કેન્દ્ર $P$ પર ચુંબકીય ક્ષેત્ર શોધો.View Solution
- 3અર્ધ-આવર્તન રીત થી ગેલ્વેનોમીટરનો અવરોધ માપવાના પ્રયોગમાં, આક્રુતિમાં દર્શાવ્યા અનુસાર, $1 / \theta$ વિધુત અવરોધ પેટીનો અવરોધ ($R$) નો આલેખ મળે છે. ગેલ્વેનોમીટર માટે ગુણવતા અંક (figure of merit) . . . . . .$\times 10^{-1} \mathrm{~A} /$ વિભાગ મળે છે. [ઉદગમનું emf $2V$ છે]View Solution
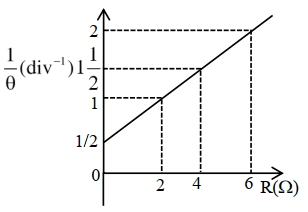
- 4વિદ્યુતભારીત કણ ચુંબકીયક્ષેત્ર $45^\circ$ના ખૂણે અમુક વેગથી દાખલ થાય તો તેનો ગતિપથ ....View Solution
- 5View Solutionવિદ્યુતપ્રવાહ ધારિત તારમાં કુલ વિદ્યુતભાર શૂન્ય છે તેમ છતાં ચુંબકીય ક્ષેત્ર તેના પર બળ લગાટે છે, કારણ કે ચુંબકીય ક્ષેત્ર
- 6બે તાર $AOB$ અને $COD$ ને લંબ રાખીને તેમાંથી $ {i_1} $ અને $ {i_2} $ પ્રવાહ પસાર કરવામાં આવે છે.તો બિંદુ $O$ થી $ABCD$ સમતલને લંબ $a$ અંતરે બિંદુ $P$ આગળ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 7$30$ કાપા ધરાવતા ગેલ્વેનોમીટરની વિધુતપ્રવાહ સંવેદીતા $20\,\mu A$ કાપા. ક્રમની છે. તેનો અવરોધ $25\, \Omega$ નો છે.$1$ એમ્પિયર પ્રવાહ માપવા માટે, તમે તેને કેવી રીતે એમિટરમાં ફેરવશો.View Solution
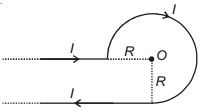
- 8આપેલ બંધારણને કારણે કેન્દ્ર $O$ પાસે કેટલું ચુંબકીય ક્ષેત્ર છે ?View Solution
- 9લાંબા પ્રવાહધારીત તારથી $4 \,cm$ ના અંતરે રહેલા બિંદુ $P$ પર પ્રેરિત ચુંબકીયક્ષેત્ર ${10^{ - 8}}\;T$ છે. સમાન પ્રવાહથી $12\, cm$ અંતરે રહેલ બિંદુ પરનું પ્રેરિત ક્ષેત્ર કેટલું થાય?View Solution
- 10દર્શાવ્યા પ્રમાણે $I$ વિદ્યુતપ્રવાહ ધરાવતા ખૂબ જ લાંબા સીધા તારને સમાંતર વિદ્યુતભાર $Q$ ગતિ કરે છે. વિદ્યુતભાર પર લાગતું બળ કઈ દિશામાં છે ?View Solution