નીચે આપેલા પદાર્થોને એક ઢાળ પર નીચેથી ઉપર તરફ (સરક્યાં વગર) ભ્રમણ કરવવામાં આવે છે
$(i)$ $R$ ત્રિજ્યાની રિંગ
$(ii)$ $\frac {R}{2}$ ત્રિજ્યાનો ઘન નળાકાર અને
$(iii)$ $\frac {R}{4}$ ત્રિજ્યાનો ઘન ગોળો
જો ઢાળના તળિયે બધાના દ્રવ્યમાન કેન્દ્રનો વેગ સમાન હોય તો તેમના દ્વારા પ્રાપ્ત થતી મહત્તમ ઊંચાઈનો ગુણોત્તર કેટલો થાય?
JEE MAIN 2019, Diffcult
Download our app for free and get started
b
\(\frac{1}{2}\left( {m + \frac{1}{{{R^2}}}} \right){v^2} = mgh\)
\(\frac{1}{2}\left( {m + \frac{1}{{{R^2}}}} \right){v^2} = mgh\)
If radius of gyration is, then
\(h = \frac{{\left( {1 + \frac{{{k^2}}}{{{R^2}}}} \right)}}{{2g}};\frac{{{k_{ring}}}}{{{R_{ring}}}} = 1,\frac{{{k_{solid\,cylinder}}}}{{{R_{solid\,cylinder}}}} = \frac{1}{{\sqrt 2 }}\)
\(\frac{{{k_{solid\,sphere}}}}{{{R_{solid\,sphere}}}} = \sqrt {\frac{2}{5}} \)
\({H_1}\,:\,{h_2}\,:\,{h_3}\,::\left( {1 + 1} \right)\,:\,\left( {1 + \frac{1}{2}} \right):\left( {1 + \frac{2}{5}} \right)::20\,:\,15\,:\,14\)
Therefore most appropriate option is \((B)\)
Although which is not in correct sequence.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
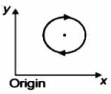
- 1View Solutionએક કણ વર્તુળમાં નિયમિત ઝડપે નીચે દર્શાવ્યા પ્રમાણે પરિભ્રમણ કરી રહ્યોં છે. ઉગમબિંદુના સંદર્ભમાં કણનું કોણીય વેગમાન શું થાય?
- 2$5\ kg $ દળ અને $30\ cm$ ત્રિજ્યાનો નળાકાર તેની અક્ષ પર મુક્ત પણે ભ્રમણ કરી શકે છે તે $3\ kg\ m^2 s^{-1}$ નો પ્રારંભિક કોણીય આપાઘાત અનુભવે છે અને દર $4\ s$ બાદ આઘાત મેળવે છે. પ્રારંભિક આઘાતનો $ 30\ s$ બાદ નળાકારનો કોણીય ઝડપ ........ $\ rad/s$ થશે. નળાકાર પ્રારંભમાં સ્થિર છે.View Solution
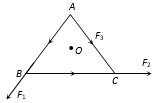
- 3$ABC$ એ સમબાજુ ત્રિકોણ છે, જેનું કેન્દ્ર $O$ છે. $\vec{F}_{1}, \vec{F}_{2}$ અને $\vec{F}_{3}$ એ અનુક્રમે $AB, BC$ અને $AC$ બાજુ પર લાગતાં બળો છે. જો $O$ ને અનુલક્ષીને કુલ ટોર્ક શૂન્ય હોય, તો $\vec{F}_{3}$ નું મૂલ્ય કેટલું હશે?View Solution
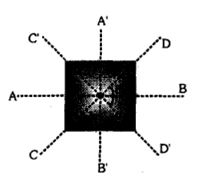
- 4ધારો કે નિયમ ચોરસ પ્લેટના કેન્દ્રમાંથી પસાર થતી અને તેની બે બાજુઓને સમાંતર અક્ષ $AB $ પર જડત્વની ચાકમાત્રા $I$ છે. $CD$ એ ચોરસના સમતલમાં છે અને $AB$ સાથે ખૂણો બનાવે છે. $CD$ અક્ષ પર પ્લેટની જડત્વની ચાકમાત્રા.......... છે.View Solution
- 5એક સળિયાની તેના દ્રવ્યમાનકેન્દ્રમાંથી પસાર થતી તેને લંબ એવી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $\frac{1}{{12}}M{L^2}$ છે. હવે સળિયાને મધ્યમાંથી એવી રીતે વાળવામાં આવે છે કે જેથી બનતા બે ભાગ તે જ સમતલમાં નો ખૂણો બનાવે છે. તો આ તંત્રની તે જ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 6View Solutionએક નિશ્ચિત બિંદુની આસપાસ સમતલમાં કોઈ દળ ભ્રમણ કરે છે, તેનું કોણીય વેગમાન કઈ દિશામાં હશે?
- 7View Solutionતંત્રને સમતોલન સ્થિતિમાં રાખવા માટે તેના પર લાગતા ટોર્કને સંતુલિત કરવું પડે . આ વિધાન સાચું કરવા માટે ટોર્ક ક્યાં લેવું પડે ?
- 8$20 \,{cm}$ ત્રિજ્યા અને $10\, {kg}$ દળ ધરાવતી ઘન તકતી તેના વર્તુળાકાર સમતલને લંબ અને તેના દ્રવ્યમાનકેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $600\, {rpm}$ ના કોણીય વેગથી ફરે છે. તકતીને $10\, {s}$ માં સ્થિ કરવા માટે જરૂરી ટોર્ક ($......\, \pi \times \,10^{-1}\, {Nm}$ માં) કેટલું હશે?View Solution
- 9$200\, kg$ના પ્લેટફોર્મના પરિઘ પર $80\, kg$ નો માણસ હોય ત્યારે તેની અક્ષને અનુલક્ષીને કોણીય ઝડપ $5\;rpm$ છે. હવે માણસ ચાલીને કેન્દ્ર પર જાય ત્યારે તે પ્લેટફોર્મની કોણીય ઝડપ ....... $rpm$View Solution
- 10કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ તેવી અક્ષને અનુલક્ષીને એક પાતળી નિયમિત તકતીની ચક્રાવર્તન ત્રિજ્યા અને તકતીના વ્યાસને ફરતે ચક્રાવર્તન ત્રિજ્યાનો ગુણોતર $......$ હશે.View Solution