વિધાન $I$: જ્યારે પ્રવાહીની ઝડપ દરેક સ્થાને શૂન્ય હોય તો કોઈ બે બિંદૂઓ વચ્ચેનો દબાણ઼ તફ઼ાવત સમી, $P_1-P_2=\rho g\left(h_2-h_1\right)$ ઊપર આધાર રાખે છે.
વિધાન $II$ : દર્શાવેલ વેન્ચ્યુમીટરમાં $2 \mathrm{gh}=v_1^2-v_2^2$ છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય ઉત્તર પસંદ કરો :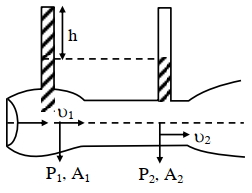
Applying Bernoulli's equation
\(\mathrm{P}_1+\rho \mathrm{gh}_1+\frac{1}{2} \rho v_1^2=\mathrm{P}_2+\rho \mathrm{gh}_2+\frac{1}{2} \rho v_2^2\)
\(\left[h_1 \& h_2\right.\) are height of point from any reference level]
\(\text { Given } \mathrm{V}_1=\mathrm{V}_2=0 \text { (for statement-1) }\)
\(\therefore \mathrm{P}_1-\mathrm{P}_2=\rho \mathrm{g}\left(\mathrm{h}_2-\mathrm{h}_2\right)\)
For statement-2
\(\mathrm{P}_1+\frac{1}{2} \rho v_1^2=\mathrm{P}_2+\frac{1}{2} \rho v_2^2\)
\(\mathrm{P}_1-\mathrm{P}_2=\rho \mathrm{gh}\)
\(\mathrm{P}_1-\mathrm{P}_2=\frac{1}{2} \rho v_2^2-\frac{1}{2} \rho v_1^2\)
\(\rho \mathrm{gh}=\frac{1}{2} \rho v_2^2-\frac{1}{2} \rho v_1^2\)
\(2 \mathrm{gh}=\mathrm{v}_2^2-\mathrm{v}_1^2\)
Hence answer \((4)\)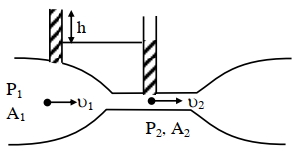
Download our appand get started for free
Similar Questions
- 1વિમાનની પાંખની ઉપર અને નીચે હવાની ઝડપ $120\, m/s $ અને $90 \,m/s$ છે.હવાની ઘનતા $1.3\, kg\, per\, metre^{3} $ છે.પાંખ $10\, m$ લંબાઇ અને $2 \,m$, પહોળાઇ ઘરાવતી હોય તો વિમાનની પાંખની ઉપર અને નીચે લાગતા દબાણનો તફાવત ......... $Pascal$ થાય.View Solution
- 2નદીમાં પાણીના ઉપરના સ્તરનો વેગ $36 \,km / h$ છે. જો પાણીના સમક્ષિતિજ સ્તરો વચ્ચે સ્પર્શીય-પ્રતિબળ $10^{-3} N / m ^{2}$ હોય તો નદીની ઉંડાઈ.......... $m$ હશે.View Solution
(પાણીનો શ્યાનતા અંક $=10^{-2} \,Pa . s$ છે.)
- 3તરલનો શ્યાનતા ગુણાંક $0.02$ ધરાવતા તરલને $20 \,m ^2$ જેટલો આડછેદનું ક્ષેત્રફળ ધરાવતા કન્ટેનરમાં ભરવામાં આવે છે. શ્યાનતાબળ બે સ્તરો વચ્ચે $1 \,N$ જેટલું હોય તો વેગ પ્રચલન ......... $s^{-1}$View Solution
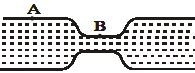
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે એક સમક્ષિતિજ નળીમાંથી પાણી વહે છે. $\mathrm{A}$ અને $\mathrm{B}$ બિંદુ જેમના આડછેડના ક્ષેત્રફળ અનુક્રમે $40\; \mathrm{cm}^{2}$ અને $20\; \mathrm{cm}^{2}$ છે, તેમની વચ્ચે દબાણનો તફાવત $700\; \mathrm{Nm}^{-2}$ છે.તો નળીમાંથી દર સેકન્ડે પસાર થતાં પાણીનું કદ . ........ $\mathrm{cm}^{3} / \mathrm{s}$ હશે.View Solution
- 5એક પ્રવાહી એક સમક્ષિતિજ નળી કે જેનો આડછેદ બદલાતો હોય તેમાં જે સ્થાને $P$ પાસ્કલ દબાણ હોય ત્યાં $v\;ms^{-1}$ વેગથી વહે છે. બીજા સ્થાને જ્યાં દબાણ $\frac{ P }{2}$ હોય ત્યાં તેનો વેગ $V\;ms^{-1}$ છે. જો પ્રવાહીની ઘનતા $\rho\, kg\, m ^{-3}$ અને પ્રવાહ ધારારેખી હોય તો $V$ કેટલો હશે?View Solution
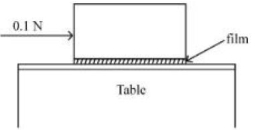
- 6આકૃતિમાં દર્શાવ્યા અનુસાર $0.20\,m ^2$ ના બેઝ (તળીયા) નું ક્ષેત્રફળ ધરાવતા એક ધાતુના ચોસલાને ટેબલ ઉપર મૂકવામાં આવેલ છે. એક $0.25\,mm$ ની પ્રવાહીની કપોટીને બ્લોક (ચોસલું) અને ટેબલની વચ્યે દાખલ કરવામાં આવે છે. બલોકને $0.1\,N$ ના સમક્ષિતિજ બળ વડે ખેંચવામાં આવે છે અને તે અચળ ઝડપથી ગતિ કરે છે. જો પ્રવાહીની સ્નિગ્ધતા $5.0 \times 10^{-3}\;Pa-s$ હોય તો બ્લોકની ઝડપ (લગભગ) $...........\times 10^{-3}\,m / s$ હશે.View Solution
- 7પાણીની ટાંકીના તળિયે છિદ્ર છે.તળિયે કુલ દબાણ $3\, atm (1\, atm = 10^{5}N/m^{2})$ છેે.તો છિદ્રમાંથી બહાર આવતા પાણીનો વેગ કેટલો થાય?View Solution
- 8$R$ ત્રિજયાના નક્કર ગોળાની અંદર $r$ ત્રિજ્યાનો પોલો ભાગ છે જે લાકડાના વહેરથી ભરેલો છે.નક્કર અને લાકડાના વહેરની સાપેક્ષ ઘનતા $2.4$ અને $0.3$ છે.સંપૂર્ણ કદ પાણીની અંદર હોય તે રીતે ગોળાને તરવા માટે નક્કર અને લાકડાના વહેરના દળનો ગુણોત્તર કેટલો હોવો જોઈએ?View Solution
- 9અમુક ઊંડાઈ પર સબમરીન પર લાગતું દબાણ $3 \times 10^{5}\;Pa$ છે. જો ઊંડાઈ બમણી કરવામાં આવે તો સબમરીન પર લાગતા દબાણમાં કેટલો પ્રતિશત વધારો થશે?(વાતાવરણનું દબાણ $=1 \times 10^{5}\; Pa$, પાણીની ઘનતા $=10^{3}\, kg \,m ^{-3}, \;g =10 \,ms ^{-2}$ )View Solution
- 10$A$ આડછેદનું ક્ષેત્રફળ ધરાવતા નળાકાર પાત્રમાં $h$ ઊંચાઈ સુધી પાણી ભરેલ છે.તેના તળિયે $a$ ત્રિજ્યાનું કાણું છે તો પાત્રને ખાલી થતાં કેટલો સમય લાગે?View Solution
