$A$ આડછેદનું ક્ષેત્રફળ ધરાવતા નળાકાર પાત્રમાં $h$ ઊંચાઈ સુધી પાણી ભરેલ છે.તેના તળિયે $a$ ત્રિજ્યાનું કાણું છે તો પાત્રને ખાલી થતાં કેટલો સમય લાગે?
JEE MAIN 2014, Diffcult
b
Let the rate of falling water level be \( - \frac{{dh}}{{dt}}\)
Let the rate of falling water level be \( - \frac{{dh}}{{dt}}\)
Initially at \(t = 0\,;\,h = h\)
\(t = t\,;h = 0\)
\(Then,\,A\left( { - \frac{{dh}}{{dt}}} \right) = \pi {a^2}.v\)
\(\left[ {Velocity\,of\,efflux\,of\,liquid\,v = \sqrt {2gh} } \right]\)
Integrating both sides
\(\int\limits_0^t {dt = - \frac{A}{{\sqrt {2g} \pi {a^2}}}{{\int\limits_h^0 h }^{ - 1/2}}dh} \)
\(\left[ t \right]_0^t = - \frac{A}{{\sqrt {2g} \pi {a^2}}} \cdot \left[ {\frac{{{h^{1/2}}}}{{1/2}}} \right]_h^0\)
\(t = \frac{{\sqrt 2 A}}{{\pi {a^2}}}\sqrt {\frac{h}{g}} \)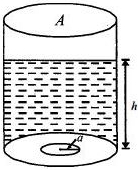
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સ્નિગ્ધ પ્રવાહીમાં $a$ ત્રિજ્યાના ગોળાનો ટર્મિનલ વેગ કોના સમપ્રમાણમાં હોય?View Solution
- 2હવામાં સીસાા (લીડ) ગઠ્ઠાને વહન કરતી વખતે એક સ્પ્રિંગ બેલેન્સ $200 \,gF$ વાંચે છે. જો હવે સિસાને ખારા પાણીના દ્રાવણમાં તેના અડધા કદ જેટલું ડૂબાડવામાં આવે, તો સ્પિંગ બેલેન્સનું નવું વાંચન ......... $gF$ હશે ? સિસા (લીડ) અને ખારા પાણીનું વિશિષ્ટ ગુરુત્વ અનુક્રમે $11.4$ અને $1.1$ છે.View Solution
- 3હવાનો પરપોટો તળાવમાં તળિયાથી સપાટી સુધી ઉપર ચઢે છે. જો તેની ત્રિજ્યા $200\%$ જેટલી વધે છે અને વાતાવરણનું દબાણ એ $H$ ઊંચાઈના પાણીના સ્તંભ જેટલું છે તો તળાવની ઊંંચાઈ ........ $H$ છે.View Solution
- 4$16 \,cm ^{2}$ જેટલું સમાન આડછેદનું ક્ષેત્રફળ ધરાવતા બે નળાકારીય વાસણો (પાત્રો)માં અનુક્રમે $100 \,cm$ અને $150 \,cm$ ઊંચાઈ સુધી પાણી ભરવામાં આવેલ છે. આ પાત્રોને જોડવામાં આવે છે કે જેથી તેઓમાં પાણીનું સ્તર સમાન ઊંચાઈએ થાય. આ પ્રક્રિયા દરમિયાન ગુરુત્વાકર્ષણને કારણે થતું કાર્ય ..........$J$ થશે. [પાણીની ધનતા $=10^{3} \,kg / m ^{3}$ અને $g =10 \,ms ^{-2}$ લો.]View Solution
- 5એક ભૂંગળી (straw) દ્વારા ખેચતા વિદ્યાર્થીના ફેફસાનું દબાણ $750\, mm\, of\, Hg$ (ઘનતા $= 13.6\, gm/cm^3$) જેટલું ઘટે છે.ભૂંગળી દ્વારા તે ગ્લાસમાંથી ....... $cm$ ઊંડાઈનું પાણી પીઇ શકે.View Solution
- 6જમીન પર રાખેલ ટાંકીમાં $10\,m$ ઊંચાઈ સુધી પાણી ભરેલ છે.તેમાં બે જમીનથી $3\, m$ અને $7\, m$ ઊંચાઈ કાણાં પડેલા છે.તો બહાર આવતા પાણી માટે શું કહી શકાય?View Solution
- 7એક હાઇડ્રોલિક ઑટોમોબાઇલ લિફ્ટ મહત્તમ $3000\, kg$ દળની કારને ઊંચકવા માટે બનાવેલી છે.આ વજન ઊંચકતા પિસ્ટનના આડછેદનું ક્ષેત્રફળ $425\, cm^2$ છે. આ પિસ્ટનને કેટલું મહત્તમ દબાણ સહન કરવું પડશે ?View Solution
- 8જ્યારે એલિવેટર ઉપરની તરફ જાય છે ત્યારે તેમાં રાખેલ બેરોમીટર $76 \,cm$ રીડીંગ દર્શાવે છે. તો તેમાં ઉદભવતું દબાણ (in $cm$ of $Hg )$ કેટલુ હશે?View Solution
- 9$1$ મી પાણી ભરેલા પાત્રમાં તળીયેથી $0.25$ મી અંતરે છિદ્ર પાડતાં તેની અવધિ ...... (સેમી માં)View Solution
- 10કેશનળીને પાત્રના તળિયે જોડેલ છે,જો તેની ત્રિજયા $10\%$ વધારતાં પ્રવાહીના વહનમાં કેટલા $\%$ ફેરફાર થાય?View Solution
