નીચે પૈકી કયું વિધાન સાચું છે?
IIT 1999, Diffcult
Download our app for free and get started
d
By Vant’s Hoff equation,
By Vant’s Hoff equation,
\(\frac{{d\ln k}}{{dt}} = \frac{{\Delta {H^o}}}{{R{T^2}}}\)
or \(\ln {k_p} = - \frac{{\Delta {H^o}}}{{RT}} + I\).
Hence \((a)\) is correct \((b)\) is also correct as plot of \(log\,(X)\) vs \(time\) is linear.
\( (c) \) is wrong because \(p \propto T\) at constant volume. \((d)\) is correct by Boyle’s law.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1રેડીયો સમસ્થાનિકની અર્ધઆયુ ચાર કલાક છે. જો સમસ્થાનિકનું શરૂઆતનું દળ $200\,g$ હોય તો $24$ કલાક પછી ....... $g$ દળ બાકી રહેશે.View Solution
- 2જ્યારે તાપમાન $40^{\circ} C$ થી $30^{\circ} C$માં બદલાયું ત્યારે પ્રક્રિયા વેગમાં $3.555$ ગણો ઘટાડો થયો.ત્યારે પ્રક્રિયાની સક્રિયકરણ ઊર્જા ...............$kJ\, mol ^{-1}$ છેView Solution
[લો; $R =8.314 \,J\, mol ^{-1}\, K ^{-1}$ In $3.555=1.268$]
- 3પ્રથમ ક્રમની પ્રક્રિયાનો વિશિષ્ટ પ્રક્રિયાવેગ $10^{-2}\, sec^{-1}$ છે. તો પ્રક્રિયકના $20\, g$ ઘટીને $5\, g$ થવા માટે ........ $\sec$ લાગશે.View Solution
- 4View Solutionજો પ્રક્રિયાનો વેગ એ વેગ અચળાંક બરાબર હોય તો પ્રક્રિયાનો ક્રમ .... થશે.
- 5જો તાપમાન $20\,^oC$ થી વધી $35\,^oC$ થતા પ્રક્રિયાનો વેગ બે ગણો થતો હોય તો પ્રક્રિયાની સક્રિયકરણ ઊર્જા ........... $kJ \,mol^{-1}$ થશે.View Solution
$(R = 8.314\, J \,mol^{-1}\, K^{-1})$
- 6જ્યારે મનુષ્યના શરીરની બહારની બાજુ ઉત્સેચકોની હાજરી ના હોય તેવું પ્રયોગશાળામાં જૈવ રાસાયણિક પ્રક્રિયા કરવામાં આવે છે. ત્યારે પ્રક્રિયાનો દર $10^{-6}$ સમય જેટલો છે તો ઉત્સેચકો હાજરીમાં પ્રક્રિયાની સક્રિયકરણ ઊર્જા ...... થશે.View Solution
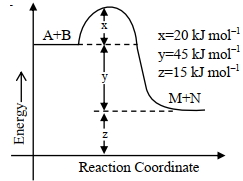
- 7નીચેના આંકડા મુજબ, પ્રક્રિયાના એન્થાલ્પી ફેરફારની તીવ્રતાView Solution
${A}+{B} \rightarrow {M}+{N}$ $......$ ${kJ} {mol}^{-1}$ બરાબર છે. (નજીકના પૂર્ણાંકમાં)
- 8$A + B \rightarrow$ નીપજો. આ પ્રક્રિયા અવલોકન મળેલ છે કે :View Solution
$(i)\,\,$ફક્ત $A$ ની શરૂઆતની સાંદ્રતા બમણી કરતા પ્રક્રિયાનો દર બમણો થાય છે.
$(ii)\,\,$$A$ અને $B$ બંનેની શરૂઆતની સાંદ્રતા બમણી કરતા પ્રક્રિયાના દરમાં $8$ ના ગુણાંકમાં ફેરફાર થાય છે.
આ પ્રક્રિયાનો દર નીચે પ્રમાણે છે.
- 9$X$ અને $Y$ વચ્ચેની પ્રક્રિયા $X$ ના સાપેક્ષમાં પ્રથમ ક્રમ અને $Y$ ના સાપેક્ષમાં શૂન્ય ક્રમ ની છે.View Solution
પ્રયોગ $\frac{[ X ]}{ mol \;L ^{-1}}$ $\frac{[ Y ]}{ mol\; L ^{-1}}$ $\frac{\text { Initial rate }}{ mol\; L ^{-1}\; min ^{-1}}$ $I$ $0.1$ $0.1$ $2 \times 10^{-3}$ $II$ $.2$ $0.2$ $4 \times 10^{-3}$ $III$ $0.4$ $0.4$ $M \times 10^{-3}$ $IV$ $0.1$ $0.2$ $2 \times 10^{-3}$ $M$ મૂલ્યનો સંખ્યાત્મક ગુણોત્તર $........$ છે. (નજીકનો પૂર્ણાંક)
- 10View Solutionપ્રથમક્રમની પ્રક્રિયા માટે વેગ અચળાંકનો એકમ નીચેના પૈકી કયો હશે ?