નીચેનામાંથી મુકતમુલક નો સ્થાયિતાનો વધતો ક્રમ કયો છે?
AIIMS 2017, Diffcult
Download our app for free and get started
b
The order of stability of free radicals
The order of stability of free radicals
${({C_6}{H_5})_3}\dot C\, > \,{({C_6}{H_5})_2}\dot CH\, > \,{(C{H_3})_3}\dot C\, > \,{(C{H_3})_2}\dot CH$
The stabilisation of first two is due to resonance and last two is due to inductive effect.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
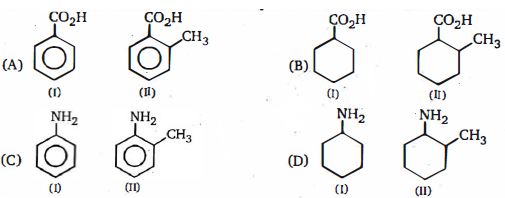
- 1નીચે આપેલી જોડીઓ માં $(A)$ અને $(B)$ માં વધુ એસિડિક અને $(C)$ અને $(D)$ માં વધુ બેઝિક શોધોView Solution
- 2નીચેના પદાર્થમાં કાર્બન - કાર્બન એક બંધ લંબાઈનો ઘટતો ક્રમ કયો છે ?View Solution
$(I)$ $CH_2 = CH - C \equiv CH$
$(II)$ $CH \equiv C - C\equiv CH$
$(III)$ $CH_3 - CH = CH_2$
$(IV) $ $CH_2 = CH - C = CH_2$
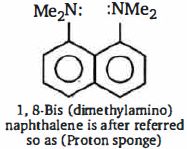
- 3તેની મૂળ પ્રબળતા $I$ - ડાયમિથાઇલ એમિનો નેપ્થાલિન કરતા વધુ $10^{10}$ છે. ઉચ્ચ બેઇઝ પ્રબળતા નું કારણ છેView Solution
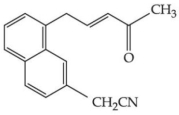
- 4આપેલ સંયોજનમાં ઈલેક્ટ્રોનઅનુરાગી કેન્દ્રોની સંખ્યા $\dots\dots\dots$ છે.View Solution
- 5View Solutionનીચેનામાંથી કયા સમઘટકીય બંધારણમાં સૌથી ઓછી ઉર્જા છે?
- 6View Solutionએસિડિક ક્ષમતાનો કયો સાચો ક્રમ છે ?
- 7View Solutionનીચેનામાંથી કઇ નીપજ ગોઠવણ કરશે?
- 8નીચેનામાંથી શેમાં નીચી $pK_a$ મૂલ્ય કઈ છે ?View Solution
- 9નીચેનાને તેમના $pK_a$ મૂલ્યોના વધતા ક્રમમાં ગોઠવોView Solution
$(x)\begin{array}{*{20}{c}}
{O\,\,\,}\\
{||\,\,\,}\\
{C{H_3} - S - O - H}\\
{||\,\,\,\,}\\
{O\,\,\,\,}
\end{array}$$\begin{array}{*{20}{c}}
{\,\,\,\,\,O}\\
{\,\,\,\,\,\,||}\\
{(y)\,\,\,C{H_3} - C - O - H}
\end{array}$$(z)\,\, CH_3 -OH$
- 10દહન ઉષ્માના ક્રમમાં નીચેના પદાર્થોને ક્રમાંકિત કરો ( મોટાભાગના ઉષ્માશોષક $\to$ ઓછામાં ઓછા ઉષ્માશોષક)View Solution
