નિયમિત ગતિ કરતી ટ્રેનની બોગી ટ્રેનથી છૂટી પડે છે અને થોડુક અંતર કાપીને સ્થિર થાય છે. તો સમાન સમયમાં બોગી અને ટ્રેન દ્વારા કપાયેલ અંતર વચ્ચેનો સંબંધ શું હોય?
Diffcult
Download our app for free and get started
b
(b) Let $'a'$ be the retardation of boggy then distance covered by it be $S$. If $u$ is the initial velocity of boggy after detaching from train (i.e. uniform speed of train)
(b) Let $'a'$ be the retardation of boggy then distance covered by it be $S$. If $u$ is the initial velocity of boggy after detaching from train (i.e. uniform speed of train)
${v^2} = {u^2} + 2as \Rightarrow 0 = {u^2} - 2as \Rightarrow {s_b} = \frac{{{u^2}}}{{2a}}$
Time taken by boggy to stop
$v = u + at \Rightarrow 0 = u - at \Rightarrow t = \frac{u}{a}$
In this time t distance travelled by train$ = {s_t} = ut = \frac{{{u^2}}}{a}$
Hence ratio $\frac{{{S_b}}}{{{S_t}}} = \frac{1}{2}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
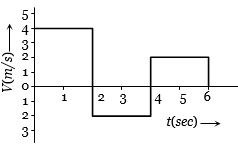
- 1એક પદાર્થનો વેગ વિરુધ્ધ સમયનો આલેખ આપેલ છે.તો પદાર્થે $6\, sec$ માં કરેલ સ્થાનાંતર અને પથલંબાઇ કેટલી હશે?View Solution
- 2$3\,km/hr$ ની ઝડપથી ગતિ કરતી નદીમાં,હોડી $5\, km/hr$ ની ઝડપથી ગતિ કરે છે.નદીની પહોળાઇ $1\, km $ છે.હોડીને નદીને પાર કરીને પાછા મૂળ જગ્યાએ આવતા કેટલા .......$min$ નો લઘુતમ સમય લાગશે?View Solution
- 3View Solutionએક દડાને ઉપર તરફ શિરોલંબ દિશામાં ફેંકવામાં આવે છે. જો હવાના અવરોધને અવગણવામાં ન આવે તો નીચેનામાથી કયો દડા માટે ઝડપ-સમય નો આલેખ દર્શાવે છે?
- 4એક કાર $200 \;m$ જેટલું અંતર કાપે છે.તે પ્રથમ અડધું અંતર $40 \;km / h$ ની ઝડપે કાપે છે. બાકીનું અડધું અંતર $v$ જેટલી ઝડપે કાપે છે.જો કારની સરેરાશ ઝડપ $48\; km / h$ હોય,તો $v$ નું મૂલ્ય ...... $km/h$ હશે.View Solution
- 5એક બલૂન $10\; m/s$ ના અચળ વેગથી ઉપર તરફ ગતિ કરે છે. જ્યારે તે જમીનની સપાટીથી $75$ મીટરની ઉંચાઈ પર હોય, ત્યારે બલૂનમાંથી સીમિત દળનો પદાર્થ છોડવામાં આવે છે. જ્યારે પદાર્થ જમીન સાથે અથડાય ત્યારે જમીનથી બલૂનની ઊંચાઈ ($m$ માં) કેટલી હશે? ($g=10 \,{m} / {s}^{2}$ લો)View Solution
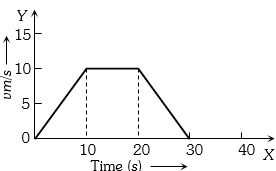
- 6આપેલ ગ્રાફ માટે પદાર્થે કાપેલ અંતર .......... $\mathrm{m}$ હશે.View Solution
- 7એક કાર અડધો સમય $80km/hr$ અને બાકીનો અડધો સમય $40 km/hr$ ની ઝડપે કાપે છે.કાપેલ કુલ અંતર $60 km$ છે.તો સરેરાશ ઝડપ કેટલા...........$km/h$ થાય?View Solution
- 8View Solutionજો એક સમય અંતરાલ પર સરેરાશ ઝડપ અને સરેરાશ વેગની તીવ્રતા સમાન હોય, તો શું હોવું જોઈએ?
- 9ટાવરની ટોચથી $10 \,m / s$ ની ઝડપે બોલ ઉપરની તરફ ફેકવામાં આવે છે અને તે $20 \,m / s$ ની ઝડપ સાથે જમીન પર પહોંચે છે. ટાવરની ઉંચાઈ ............ $m$ થાય? [$g = 10 \,m / s ^2$ લો]View Solution
- 10સુરેખ પથ પર ગતિ કરતો એક કણ અડધું અંતર $3 \,m/s$ ની ઝડપ થી કાપે છે.બાકીનું અડધું અંતર બે સમાન અંતરાલ માં અનુક્રમે $4.5 \,m/s$ અને $7.5 \,m/s$ ની ઝડપે કાપે છે. આ ગતિ દરમિયાન કણની સરેરાશ ઝડપ $(\,m/s)$ કેટલી થાય?View Solution