પાણીની અંદર વિસ્ફોટ થતાં ઉત્પન્ન થયેલ એક પરપોટાના દોલનોનો આવર્તકાળ $P^a\,d^b\,E^c$ ના સમપ્રમાણમાં છે. જ્યાં $P$ દબાણ, $d$ પાણીની ઘનતા અને $E$ વિસ્ફોટની ઉર્જા છે. તો $a,\,b$ અને $c$ ના મૂલ્યો અનુક્રમે કેટલા હશે?
Diffcult
Download our app for free and get started
a
Time period $\mathrm{T}=\mathrm{P}^{\mathrm{a}} \mathrm{d}^{\mathrm{b}} \mathrm{E}^{\mathrm{c}}$
Time period $\mathrm{T}=\mathrm{P}^{\mathrm{a}} \mathrm{d}^{\mathrm{b}} \mathrm{E}^{\mathrm{c}}$
Taking dimensions of each physical quantity.
$[\mathrm{T}]=\left[\mathrm{ML}^{-1}\mathrm{T}^{-2}\right]^{\mathrm{a}}\left[\mathrm{ML}^{-3}\right]^{\mathrm{b}}\left[\mathrm{ML}^{2} \mathrm{T}^{-2}\right]^{\mathrm{c}}$
Equating the exponents of $\mathrm{M}, \mathrm{L}$ and $\mathrm{T}$ on both the sides,
$\mathrm{M}^{\mathrm{a}+\mathrm{b}+\mathrm{T}} \mathrm{L}^{-\mathrm{a}-3 \mathrm{b}+2 \mathrm{c}} \mathrm{T}^{-2 \mathrm{a}-2 \mathrm{c}} =\mathrm{T}$
$\mathrm{a}+\mathrm{b}+\mathrm{c} =0$
$-\mathrm{a}-3 \mathrm{b}+2 \mathrm{c} =0$
$-2 \mathrm{a}-2 \mathrm{c} =1$
Solving these equations for $a$, $b$ and $c,$ we get
$a=-\frac{5}{6}, b=\frac{1}{2}$ and $\frac{1}{3}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઘન આકારના પદાર્થની ઘનતા તેની ત્રણ બાજુઓ અને દળ માપીને નકકી કરવામાં આવે છે.જો તેના દળ અને લંબાઇ માપવામાં થતી સાપેક્ષ ત્રુટીઓ અનુક્રમે $1.5 \%$ અને $1 \%$ હોય, તો ઘનતા માપવામાં થતી મહત્તમ ત્રુટિ ........ $\%$View Solution
- 2ગોળાની ત્રિજ્યા $(7.50 \pm 0.85) \,cm $ માપવામાં આવે છે. ધારો કે તેના કદમાં પ્રતિશત ત્રુટિ $x$ છે. $x$ નું મૂલ્ય નજીકના પૂર્ણાંકમાં કેટલું ($\%$ માં) હશે?View Solution
- 3લીસ્ટ $I$ સાથે લીસ્ટ $II$ યોગ્ય રીતે જોડો.View Solution
લીસ્ટ $I$ (ભૌતિક રાશી) લીસ્ટ $II$ (પારિમાણિક સૂત્ર) $(A)$ દબાણ પ્રચલન $(I)$ $\left[ M ^0 L ^2 T ^{-2}\right]$ $(B)$ ઊર્જા-ઘનતા $(II)$ $\left[ M ^1 L ^{-1} T ^{-2}\right]$ $(C)$ વિદ્યુતક્ષેત્ર $(III)$ $\left[ M ^1 L ^{-2} T ^{-2}\right]$ $(D)$ ગુપ્ત ઉષ્મા $(IV)$ $\left[ M ^1 L ^1 T ^{-3} A ^{-1}\right]$ - 4કોઈ પણ તંત્રની એન્ટ્રોપી નીચે મુજબ આપવામાં આવે છે.View Solution
${S}=\alpha^{2} \beta \ln \left[\frac{\mu {kR}}{J \beta^{2}}+3\right]$
જ્યાં $\alpha$ અને $\beta$ અચળાંક છે. $\mu, J, K$ અને $R$ અનુક્રમે મોલ, જૂલ અચળાંક, બોલ્ટ્ઝમેન અચળાંક અને વાયુ અચળાંક છે. [${S}=\frac{{dQ}}{{T}}$ લો]
નીચેનામાંથી ખોટો વિકલ્પ પસંદ કરો.
- 5એક પ્રિઝમનો પ્રિઝમ કોણ માપવા વપરાતા એક સ્પેક્ટ્રોમીટર નીચે પ્રમાણેનાં અવલોકનો દર્શાવે છે:View Solution
મુખ્ય માપનું અવલોકન : $58.5$ ડિગ્રી
વર્નિયર માપનું અવલોકન : $9$ મો કાપો મુખ્ય માપનાં એક કાપાનું મૂલ્ય $0.5$ ડિગ્રી છે. વર્નિયર માપ પરનાં કુલ $30$ કાપા છે જે મુખ્ય માપનાં $29$ કાપા બરાબર થાય છે. તેમ આપેલું છે. ઉપરોક્ત માહિતી પરથી પ્રિઝમનો પ્રિઝમ કોણ (ડિગ્રીમાં) કેટલો થાય?
- 6ભૌતિક રાશિ $x = \frac{{{a^2}{b^3}}}{{c\sqrt d }}$ માં $a,b,c$ અને $d$ માં પ્રતિશત ત્રુટિ $2\%,1\%,3\%$ અને $4\%$ હોય,તો ભૌતિક રાશિ $x$ માં પ્રતિશત ત્રુટિ ......... $\%$ થાય.View Solution
- 7માર્શિયન પધ્ધતિમાં બળ $(F)$, પ્રવેગ $(A)$ અને સમય $(T)$ ને મૂળભૂત રાશિ લેવામાં આવે તો માર્શિયન પધ્ધતિમાં લંબાઇનું પારિમાણિક સૂત્ર શું થાય?View Solution
- 8View Solutionનીચે પૈકી કઈ જોડના પરિમાણિક સૂત્ર સમાન છે?
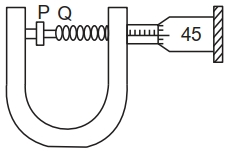
- 9સ્ક્રુગેજની મદદથી તારનો વ્યાસ માપવાના એક પ્રયોગમાં નીચે મુજબના અવલોકનો મળે છે.View Solution
$(A)$ એક પૂર્ણ પરિભ્રમણ માટે સ્ક્રુ મુખ્ય સ્કેલ ઉપર $0.5\,mm$ ખસે છે.
$(B)$ વર્તુળાકાર સ્કેલ પર કુલ $50$ કાપા છે.
$(C)$ મુખ્ય સ્કેલ પરનું અવલોકન $2.5\,mm$ છે.
$(D)$ વર્તુળાકાર સ્કેલ પરનો $45$ મો કાપો પીચ-રેખા પર આવે છે.
$(E)$ સાધનને $0.03\,mm$ જેટલી ઋણ ત્રુટી છે.
તો તારનો વ્યાસ $............\;mm$ થશે.
- 10પ્રકાશની તરંગલંબાઇ $ 0.00006\,m $ હોય,તો માઇક્રોમાં તેનું મુલ્ય .......... $microns$ થશે.View Solution