પાણીની ટાંકીમાં બે છિદ્ર છે.એક $L$ બાજુવાળુ ચોરસ છિદ્ર પાણીની સપાટીથી $y$ ઊંડાઇ પર અને બીજુ $R$ ત્રિજયાવાળુ છિદ્ર $ 4y $ ઊંડાઇ પર છે. એક સેકન્ડમાં બહાર આવતા પાણીના કદ બંને છિદ્ર માટે સમાન છે.તો $ R=$ ____
IIT 2000,AIEEE 2012, Diffcult
b
(b)Velocity of efflux when the hole is at depth h, \(v = \sqrt {2gh} \)
Rate of flow of water from square hole
\({Q_1} = {a_1}{v_1}\)= \({L^2}\sqrt {2gy} \)
Rate of flow of water from circular hole
\({Q_2} = {a_2}{v_2}\)= \(\pi {R^2}\sqrt {2g(4y)} \)
According to problem \({Q_1} = {Q_2}\)
==> \({L^2}\sqrt {2gy} = \pi {R^2}\sqrt {2g(4y)} \) \( \Rightarrow \)\(R = \frac{L}{{\sqrt {2\pi } }}\)
(b)Velocity of efflux when the hole is at depth h, \(v = \sqrt {2gh} \)
Rate of flow of water from square hole
\({Q_1} = {a_1}{v_1}\)= \({L^2}\sqrt {2gy} \)
Rate of flow of water from circular hole
\({Q_2} = {a_2}{v_2}\)= \(\pi {R^2}\sqrt {2g(4y)} \)
According to problem \({Q_1} = {Q_2}\)
==> \({L^2}\sqrt {2gy} = \pi {R^2}\sqrt {2g(4y)} \) \( \Rightarrow \)\(R = \frac{L}{{\sqrt {2\pi } }}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક લાકડાનો બ્લોક તેનું $\frac{4}{5} th$ ભાગનું કદ પાણીમાં ડૂબાયેલું રહે તેમ તરી રહ્યું છે, પરંતુ તે માત્ર બીજા પ્રવાહીમાં તરે છે. પ્રવાહીની ઘનતા કેટલી છે ? (in $kg / m ^3$ )View Solution
- 2નળાકાર પાત્રમાં પ્રવાહી ભરેલ છે.જયારે પાત્રને તેના અક્ષને અનુલક્ષીને ફેરવવામાં આવે છે.પ્રવાહી તેની બાજુ પર ચડે છે.પાત્રની ત્રિજયા $ r $ અને પાત્રની કોણીય આવૃતિ $\omega $ પરિભ્રમણ/સેકન્ડ છે. કેન્દ્ર અને બાજુ પરના પ્રવાહીની ઊંચાઇનો તફાવત કેટલો થાય?View Solution
- 3આકૃતિમાં $2.0\,cm ^2$ આડછેદનું ક્ષેત્રફળવાળા પિસ્ટન દ્વારા નળીમાંથી પ્રવાહી ધકેલાતુ દર્શાવેલ છે. નળીના બાહ્ય છેડાનું આડછેદનું ક્ષેત્રફળ $10\,mm ^2$ છે.જો પિસ્ટનને $4\,cm\,s ^{-1}$ જેટલી ઝડપથી ધકેલવામા આવે, તો બહાર જતા પ્રવાહીની ઝડપ ........ $cm\,s ^{-1}$ છે.View Solution

- 4ત્રાજવામાં મૂકેલા બે પદાર્થો પાણીમાં સમતોલનમાં રહે છે,એક પદાર્થનું દળ $36 g$ અને ઘનતા $9 \,g / cm^{3}$છે,જો બીજા પદાર્થનું દળ $48 \,g$ હોય,તો તેની ઘનતા ..... $g / cm^{3}$ હશે.View Solution
- 5$10^3 \,kg / m ^3$ ધનતા અને શ્યાનતા ગુણાંક $8 \times 10^{-2} \;decapoise$ ધરાવતું પ્રવાહી $2 \,cm$ ત્રિજ્યા ધરાવતી ટ્યૂબમાંથી $2 \,m / s$ ના વેગથી વહન પામે છે તો રેનોલ્ડ અંક કેટલો ?View Solution
- 6$20 \,m$ પાણીની સપાટીની નીચે તરવૈયા ઉપર લાગતું દબાણ ............. $atm$View Solution
- 7View Solutionસ્પ્રે કોના નિયમ પર આધાર રાખે છે.
- 8બે બાજુ $A$ અને $A'$ આડછેદની ક્ષેત્રફળ ધરાવતી નળી માથી પાણી વહે છે જ્યાં આડછેદના ક્ષેત્રફળનો ગુણોત્તર $A/A'=5$. જો નળીના બંને છેડા વચ્ચે દબાણનો તફાવત $3 \times 10^5\, N\, m^{-2}$ હોય તો નળીમાં પાણી .......... $m s^{-1}$ ના વેગથી પ્રવેશ કરે?(ગુરુત્વાકર્ષણની અસરને અવગણો)View Solution
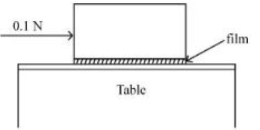
- 9આકૃતિમાં દર્શાવ્યા અનુસાર $0.20\,m ^2$ ના બેઝ (તળીયા) નું ક્ષેત્રફળ ધરાવતા એક ધાતુના ચોસલાને ટેબલ ઉપર મૂકવામાં આવેલ છે. એક $0.25\,mm$ ની પ્રવાહીની કપોટીને બ્લોક (ચોસલું) અને ટેબલની વચ્યે દાખલ કરવામાં આવે છે. બલોકને $0.1\,N$ ના સમક્ષિતિજ બળ વડે ખેંચવામાં આવે છે અને તે અચળ ઝડપથી ગતિ કરે છે. જો પ્રવાહીની સ્નિગ્ધતા $5.0 \times 10^{-3}\;Pa-s$ હોય તો બ્લોકની ઝડપ (લગભગ) $...........\times 10^{-3}\,m / s$ હશે.View Solution
- 10જો વહનનો વેગ $4 \,m / s$ હોય તો વેલોસિટી હેડ .......... $m$ ?View Solution
