પાતળી ધાતુની તકતીમાંથી $ R$ ત્રિજ્યાનું વર્તૂળાકાર કાપી નાંખેલ છે. $R/2$ ત્રિજ્યાનું છિદ્ર આ વર્તૂળમાંથી કરવામાં આવે છે. આ રીતે વર્તૂળની રીમને સ્પર્શેં છે. તેનું મૂળ કાપ્યા વગરના ભાગના દ્રવ્યમાન કેન્દ્રથી અંતર શોધો.
Medium
a
વાસ્તવિક કાપ્યા વગરના ભાગ સાથે આ છિદ્રને ઋણ દળ તરીકે ગણતાં (જ્યારે બંને એક સાથે જાડાયેલા હોય ત્યારે છીદ્ર પર કોઈ હોતું નથી) સમમિતિ પરથી, દ્રવ્યમાન કેન્દ્ર અક્ષ પર રહેલું છે.
વાસ્તવિક કાપ્યા વગરના ભાગ સાથે આ છિદ્રને ઋણ દળ તરીકે ગણતાં (જ્યારે બંને એક સાથે જાડાયેલા હોય ત્યારે છીદ્ર પર કોઈ હોતું નથી) સમમિતિ પરથી, દ્રવ્યમાન કેન્દ્ર અક્ષ પર રહેલું છે.
તેથી આકૃતિમાં દર્શાવ્યા પ્રમાણે\(xCM = 0.\)
કેન્દ્ર પર ઊગમબિંદુ લેતાં વાસ્તવિક વર્તુળનું દળ \(m\) ધારો.
વાસ્તવિક કાપ્યા વગરનો ભાગ \(Mass m_1 = m \) અને \(CM\) નું સ્થાન\( (0, 0) \)
છિદ્ર નું ઋણ \(\,Mass\,\,{{\text{m}}_{\text{2}}}\, = \,\,\frac{m}{4}\,\) અને \({\text{ CM}}\) નું સ્થાન \(\left( {0,\,\,\frac{R}{2}} \right)\)
તેથી \({{\text{y}}_{{\text{CM}}}}\, = \,\,\,\frac{{{m_1}{y_1}\, + \,\,{m_2}{y_2}}}{{{m_1}\, + \,\,{m_2}}}\)
\( = \,\,\,\frac{{m(0)\,\, + \,\,\left( { - \frac{m}{4}} \right)\left( {\frac{R}{2}} \right)}}{{m\,\, + \,\,\left( { - \frac{m}{4}} \right)}}\,\,\, = \,\,\frac{R}{6}\)
દ્રવ્યમાન કેન્દ્ર નું સ્થાન \(\,\,\left( {0,\,{\text{ - }}\frac{{\text{R}}}{{\text{6}}}} \right)\)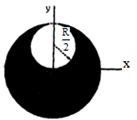
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$l$ લંબાઈના એક સળિયાના દ્રવ્યમાન કેન્દ્રથી $\frac{l}{4}$ અંતરે તેને લંબ અક્ષ માથી પસાર થતી અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા કેટલી થાય?View Solution
- 2$30^o $ ના ખૂણા ધરાવતા ઢાળ પરથી નકકર ગોળો ગબડે ત્યારે,તેનો પ્રવેગView Solution
- 3એક પાતળી ચોરસ તકતી જેનું દળ $m$ અને બાજુની લંબાઈ $a$ છે તેના વિકર્ણને અનુલક્ષીને જડત્વની ચાકમાત્રા $I$ હોય તો ...View Solution
- 4નિયમિત કોણીય પ્રવેગ સાથે ભ્રમણ કરતો એક પદાર્થ શરૂ થયા પછી $5 \,s$ માં $100 \pi$ (રેડીયન) પૂર્ણ કરે છે. તો $5 \,s$ પછી તેની કોણીય ઝડપ $rev/s$ ........ $\pi$ થશે?View Solution
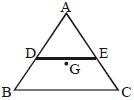
- 5$ABC$ સમબાજુ ત્રિકોણ તકતી છે.$O$ અને $E$ એ $AB$ અને $AC$ના મધ્યબિંદુ છે.$G$ એ કેન્દ્ર છે. $G$ માંથી પસાર થતી અને સમતલ $ABC$ને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાક્માત્રા $I _{0}$ છે.જો $ADE$ ભાગને દૂર કરવામાં આવે છે ત્યારે વધેલા ભાગની જડત્વની ચાક્માત્રા તે જ અક્ષને અનુલક્ષીને $\frac{ NI _{0}}{16}$ હોય તો $N=......$View Solution
- 6એક વ્હીલએ તેની સમાંતર અક્ષને અનુલક્ષીને $4 \,kg m ^2$ ની જડત્વની ચાક્રમાત્રા ધરાવે છે. તે અક્ષનો અનુલક્ષીને $240 \,rpm$ ની ઝડપે ભ્રમણ કરે છે. તો એક મિનિટ માં વ્હીલનું પરિભ્રમણ અટકાવવા માટે ........... $Nm$ ટોર્કની જરુર પડે?View Solution
- 7એક $M$ દળની અને $R$ ત્રિન્યા વાળી વર્તુળાકાર તક્તિ સમક્ષિતિજ સમતલમાં તેના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ, $\omega$ કોણીય વેગથી ભ્રમણ કરે છે. જો સમાન પરિમાણ પરંતુ $\mathrm{M} / 2$ દળની બીજી તક્તિને પ્રથમ તક્તિ પબ સમાક્ષી રીતે હળવેકથી મૂકવામાં આવે તો તંત્રનો નવો કોણીય વેગ. . . . . . .છે.View Solution
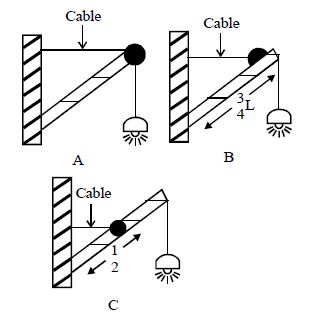
- 8આકૃતિમાં દર્શાવ્યા પ્રમાણે કોઈ નિયમિત $L$ લંબાઈના થાંભલાના છેડે $M$ દળની સ્ટ્રીટ લાઇટ અલગ અલગ સ્થિતિમાં લટકાવેલી છે. તોView Solution
- 9સમાંતર અક્ષ પ્રમેય $I = {I_g} + M{d^2}$ અનુસાર હોય તો $I$ અને $d$ વચ્ચે નીચેનામાથી શું સાચું છે ?View Solution
- 10View Solutionજ્યારે ગબડતો પદાર્થ એ લીસી સમક્ષિતિજ સપાટી પર પ્રવેશ કરે છે, ત્યારે તે .........
