प्रिज्म के किसी अपवर्तक पृप्ठ पर किसी प्रकाश किरण के लिए आपतन कोण का मान $45^{\circ}$ है। प्रिज्म कोण का मान $60^{\circ}$ है। यदि यड किरण प्रिज्म से न्यूनतम विचतित होती है, तो न्यूनतम विचलन कोण तथा प्रिज्म के प्रदार्थ का अपवर्त्तनांक क्रमश: हैः
[2016]
Download our app for free and get started
दिया है,
आपत्तित कोण $i=45^{\circ}$,
प्रिज्म कोण $A =60^{\circ}$;
न्यूनतम विचलन कोण
$ \delta_{ m }=2 i - A =30^{\circ} $
प्रिज्म के पदार्थ का अपवर्तनांक
$ \mu=\frac{\sin \left(\frac{A+\delta_m}{2}\right)}{\sin A / 2}$
$=\frac{\sin 45^{\circ}}{\sin 30^{\circ}}=\frac{1}{\sqrt{2}} \cdot \frac{2}{1}=\sqrt{2} $
आपत्तित कोण $i=45^{\circ}$,
प्रिज्म कोण $A =60^{\circ}$;
न्यूनतम विचलन कोण
$ \delta_{ m }=2 i - A =30^{\circ} $
प्रिज्म के पदार्थ का अपवर्तनांक
$ \mu=\frac{\sin \left(\frac{A+\delta_m}{2}\right)}{\sin A / 2}$
$=\frac{\sin 45^{\circ}}{\sin 30^{\circ}}=\frac{1}{\sqrt{2}} \cdot \frac{2}{1}=\sqrt{2} $
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1एक प्रिज्म जिसका कोण $A$ है, के एक समतल पर एक किरण आपतन कोण बनाते हुए आती है तथा वह दूसरे समतल के लम्बवत बाहर निकलती है। यदि प्रिज्म के पदार्थ का अपवर्तनांक $\mu$ हो तो आपतन कोण $i$ का मान लगभग होगा:View Solution
- 2उत्तल लेंस के लिए बैगनी तथा लाल प्रकाश के लिए फोकस दूरियां $f_V$ तथा $f_R$ है। अवतल लेंस के लिए यही फोकस दूरियां $F _{ V }, F _{ R }$ हैं । तोView Solution
- 3$60^{\circ}$ के किसी प्रिज्म पर प्रकाश की एक किरण अल्पतम् विचलन की स्थिति पर आपतित होती है। पहले पाश्र्व (फलक) पर (अर्थात् आपतन पाश्र्व पर) अपवर्तन कोण हैView Solution
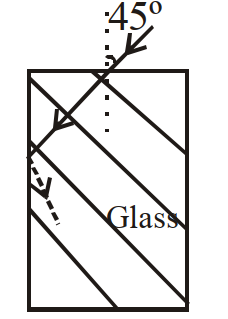
- 4View Solutionएक प्रकाश किरण काँच के गुटके पर चित्रानुसार पड़ती है। यदि उर्ध्वाधर पृष्ठ से पूर्ण आंतरिक परावर्तन हुआ हो तो काँच का अपवर्तनांक होगा :
- 5जब $1.47$ अपवर्तनांक के कॉंच के किसी उभयोत्तल लैंस को किसी द्रव में डुबाया जाता है तो, यह एक समतल शीट $($ परत $)$ की भॉंति व्यवहार करता है। इसका तात्पर्य यह है कि द्रव का अपवर्तनांक हैःView Solution
- 6एक लेंस, प्रकाश स्रोत्र तथा दीवार के बीच रखा है। यह लेंस के दो भिन्न स्थितियों दीवार पर $A _1$ तथा $A _2$ क्षेत्रफल के दो प्रतिबिम्ब बनाता है। प्रकाश स्रोत्र का क्षेत्रफल होगाView Solution
- 7दो माध्यमों $M_1$ और $M_2$ में प्रकाश की चाल क्रमशः $1.5 \times 10^8 m / s$ और $2.0 \times 10^8 m / s$ है। प्रकाश की एक किरण माध्यम $M_1$ से $M_2$ में $i$ आपतन कोण पर प्रवेश करती है। यदि इस किरण का पूर्ण आतंरिक परावर्तन हो जाता है तो, ' $i$ ' का मान हैView Solution
- 8सामान्य नेत्त्र में कौर्निया $($स्वच्छ मंडल$)$ की अभिसारी शक्ति $40 D$ है तथा कार्निया के पीछे नेत्र लेंस की न्यूनतम अभिसारी शक्ति $20 D$ है। इस सूचना से नेत्र के रेटिना $($दृष्टिपटल$)$ तथा लेन्स के बीच की अनुमानित दूरी होगी:View Solution
- 9View Solutionनिम्न विकिरणों में किसकी तरंगद्धर्य अधिकतम है
- 10एक पतले समतलोत्तल लैंस की वक्रता त्रिज्या 10 सेमी तथा अपवर्तनांक $1.5$ है। यदि समतल पृष्ठ को पोलिश कर दिया जाए तो यह अवतल दर्पण का काम करेगा। इसकी फोकस दूरी है:View Solution