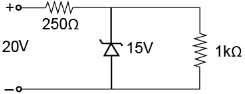
પરિપથમાં દર્શાવ્યા મુજબ, $15 \;V $ બ્રેકડાઉન વોલ્ટેજ ધરાવતા ઝેનર ડાયોડનો ઉપયોગ વોલ્ટેજ રેગ્યુલેટર તરીકે કરેલ છે. ડાયોડમાંથી પસાર થતો પ્રવાહ ($mA$ માં) કેટલો હશે?

AIPMT 2011, Medium
a
The voltage drop across \(1 \mathrm{k} \Omega=V_{z}=15 \mathrm{V}\)
The voltage drop across \(1 \mathrm{k} \Omega=V_{z}=15 \mathrm{V}\)
The current through \(1 \mathrm{k} \Omega\) is
\(I^{\prime}=\frac{15 \mathrm{V}}{1 \times 10^{3} \Omega}=15 \times 10^{-3} \mathrm{A}=15 \mathrm{mA}\)
The voltage drop across \(250 \Omega=20 \mathrm{V}-15 \mathrm{V}=5 \mathrm{V}\)
The current through \(250 \Omega\) is
\(I=\frac{5 \mathrm{V}}{250 \Omega}=0.02 \mathrm{A}=20 \mathrm{mA}\)
The current through the zener diode is
\(I_{2}=I-I^{\prime}=(20-15) \mathrm{mA}=5 \mathrm{mA}\)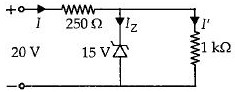
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
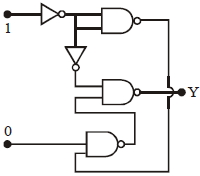
- 1આપેલ પરિપથમાં $Y$ નું મૂલ્ય શું મળે?View Solution
- 2$NPN$ ટ્રાન્ઝિસ્ટરમાં પરિપથમાં કલેક્ટર વિદ્યુતપ્રવાહ $10$ છે. જો $95\%$ ઈલેક્ટ્રોન બહાર નીકળીને કલેક્ટર સુધી પહોંચી ગયા હોય, તો બેઝ વિદ્યુતપ્રવાહ કેટલા ....$mA$ હશે?View Solution
- 3View Solutionધાતુ પદાર્થ અને અર્ધવાહક પદાર્થના તાપમાનમાં ફેરફાર થતાં તેમના અવરોધમાં થતો ફેરફાર કેમ અલગ અલગ પ્રકારનો હોય છે ?
- 4$N_A$ એ એસ્પેટર (સ્વીકારનાર) પરમાણુની ઘનતા હોય અને $N_D$ એ ડોનર પરમાણુની ઘનતા હોય તો $n_e$ વાહક $n_h$ જે ઈલેક્ટ્રોન અને હોલની ઘનતા શું હશે ?View Solution
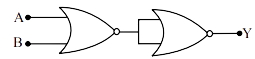
- 5નીચે દર્શાવેલ લોજિક પરિપથ માટે તમામ સંભવિત $A$ અને $B$ મૂલ્યો માટે $Y$ આઉટપુટને કયા ટુથટેબલ વડે દર્શાવી શકાય છે?View Solution
- 6$p-n$ જંકશન ડાર્યોડમાં પોટેન્શિયલ બેરિયર ઉત્પન્ન થવાનું કારણView Solution
- 7View Solutionઅંર્તગત અર્ધવાહક વિદ્યુતની દ્રષ્ટિએ તટસ્થ હોય છે.તો બર્હિગત અર્ધવાહક વિદ્યુતની દ્રષ્ટિએ
- 8શ્રેણી $LCR$ પરિપથમાં, કેપેસીટન્સનું મૂલ્ય $C$ માંથી $4 C$ બદલવામાં આવે છે. તેની અનુનાદ આવૃતિ બદલાય નહી તે માટેના નવા ઈનડકટરનેView Solution
- 9$1\;k\Omega$($h_{fe} = 50$ અને $h_{oe} = 25\;\mu A/V$) લોડ અવરોધ ધરાવતા કોમન એમીટર અમ્પ્લિફાયરનો પ્રવાહ ગેઇન કેટલો મળે?View Solution
- 10$Ge $ ની ફોરબીડન ઊર્જાગેપ ....... $eV.$View Solution
