પ્રકિયા $2{C_{\left( {graphite} \right)}} + 2{H_{2\left( g \right)}} \to {C_2}{H_{4\left( g \right)}}$ માટે એન્થાલ્પી ફેરફાર......$kJ$ ગણો.
${C_{\left( {graphite} \right)}} + {O_{2\left( g \right)}} \to C{O_{2\left( g \right)}}\,;\,\Delta H = -393.5\,kJ$
${C_2}{H_{4\left( g \right)}} + 3{O_{2\left( g \right)}} \to 2C{O_{2\left( g \right)}} + 2{H_2}{O_{\left( l \right)}}\,;\,\Delta H = - 1410.9\,kJ$
${H_{2\left( g \right)}} + 1/2{O_{2\left( g \right)}} \to {H_2}{O_{\left( l \right)}}\,;\,\Delta H = - 285.8\,kJ$
Medium
Download our app for free and get started
b
\(i)\) \(C + O _2 \longrightarrow CO _2 \quad \Delta H _i=-393.5\)
\(i)\) \(C + O _2 \longrightarrow CO _2 \quad \Delta H _i=-393.5\)
\(ii)\) \(C _2 H _4+3 O _2 \longrightarrow 2 CO _2+2 H _2 O \quad \Delta H _{ ii }=-1410.9\)
\(iii)\) \(H _2+\frac{1}{2} O _2 \longrightarrow H _2 O \quad \Delta I _{ iii }=-25.8\)
\(iv)\) \(2 C +2 H _2 \longrightarrow C _2 H _4 \Delta H =(?)\)
\(iv)\) \(=2( i )-( ii )+2 (iii)\)
\(\therefore \Delta H =2 \Delta H _{ i }-2 \Delta H _{ ii }+2 \Delta H _{ iii }\)
\(=2(-393.5)-(-1410.9)+2(-285.8)\)
\(=-787+1410.9-571.6\)
\(=1410.9-1358.6\)
\(=52.3\, kJ\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$45.0\, g$ સિલિકોનના તાપમાનમાં $6\,^oC$ નો વધારો કરવા $192\,J$ ઉષ્માની જરૂર પડે તો તેની વિશિષ્ટ ઉષ્માક્ષમતા.....View Solution
- 2$X \,gm$ ઈથેનાલ $(CH_3CHO)$ ને બોમ્બ કેલેરીમીટરમાં સળગાવે છે અને $Y$ જુલ ઉષ્મા ઉત્પન્ન થાય છે. તો .....View Solution
- 3બે સંયોજનો $x$ અને $y$ ની સર્જન એન્થાલ્પીના મૂલ્ય અનુક્રમે $-84\, kJ $ અને $-156 \,kJ$ છે,નીચેનામાંથી કયું વિધાન યોગ્ય છેView Solution
- 4પ્રક્રિયા માટેView Solution
$C _{2} H _{6} \rightarrow C _{2} H _{4}+ H _{2}$
પ્રકિયા એન્થાલ્પી $\Delta_{ r } H =...........{ kJ\, mol ^{-1}}$.
[આપેલ : બંધ એન્થાલ્પી $kJ$ $mol$ $^{-1}:C-C : 347, C = C : 611 ; C - H : 414, H - H : 436]$
- 5આપેલ :View Solution
$(i)\, {\Delta _f}{H^o}$ of $N_2O$ is $82\, kJ\, mol^{-1}$ છે,
$(ii)$ $N \equiv N,N = N,O = O$ અને $N = O$ બંધઊર્જા અનુક્રમે $946, 418, 498$ અને $607\, kJ\, mol^{- 1}$ છે. તો $N_2O$ ની સંસ્પંદન ઊર્જા ......$kJ$
- 6View Solutionઆદર્શ વાયુના ઉષ્મીય પ્રસરણ દરમ્યાન તેની.......
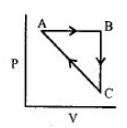
- 7એક આદર્શ વાયુ નીચે દર્શાવેલ આકૃતિ મુજબ ચક્રીય પ્રક્રમ અનુભવે છે.View Solution
$\Delta {U_{BC}} = - 5\,kJ\,mo{l^{ - 1}},{q_{AB}} = 2\,kJ\,mo{l^{ - 1}}$
$\Delta {W_{AB}} = - 5\,kJ\,mo{l^{ - 1}},{W_{CA}} = 3\,kJ\,mo{l^{ - 1}}$
$CA$ પ્રક્રમ દરમિયાન પ્રણાલી દ્વારા શોષાતી ઉષ્મા ......$kJ\,mo{l^{ - 1}}$
- 8$27^{\circ} \mathrm{C}$ પર અચળ કદે ધન બેન્ઝોઈક એસિડ ની દહનઉષ્મા $-321.30 \mathrm{~kJ}$ છે. અચળ દબાણ પર દહનઉષ્મા $(-321.30-x \mathrm{R}) \mathrm{kJ}$ છે. $x$ નું મૂલ્ય ......... છે.View Solution
- 9${I_{2\left( s \right)}}$ ની ઊર્ધ્વીકરણ ઊર્જા $57.3\, kJ\, mol^{-1}$ અને ગલન એન્થાલ્પી $15.5\, kJ\,mol^{-1}$ છે. તો ${I_2}$ ની બાષ્પાયન એન્થાલ્પી .....................$kJ\,mo{l^{ - 1}}$ થશે.View Solution
- 10નીચે આપેલા $p-V$ વક્રમાંથી ક્યું સૌથી વધારે થયેલ કાર્ય દર્શાવે છે?View Solution