પ્રક્રિયા $2 \mathrm{H}_{2}(\mathrm{g})+2 \mathrm{NO}(\mathrm{g}) \rightarrow \mathrm{N}_{2}(\mathrm{g})+2 \mathrm{H}_{2} \mathrm{O}(\mathrm{g})$ માટે અવલોકન વેગ રજૂઆત, વેગ $=\mathrm{k}_{\mathrm{f}}[\mathrm{NO}]^{2}\left[\mathrm{H}_{2}\right]$ છે. તો પ્રતિગામી પ્રક્રિયા માટે વેગ રજૂઆત જણાવો.
JEE MAIN 2020, Medium
Download our app for free and get started
d
\(\mathrm{K}_{\mathrm{eq}}=\frac{\mathrm{k}_{\mathrm{f}}}{\mathrm{k}_{\mathrm{b}}}=\frac{\left[\mathrm{N}_{2}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]^{2}}{\left[\mathrm{H}_{2}\right]^{2}[\mathrm{NO}]^{2}}\)
\(\mathrm{K}_{\mathrm{eq}}=\frac{\mathrm{k}_{\mathrm{f}}}{\mathrm{k}_{\mathrm{b}}}=\frac{\left[\mathrm{N}_{2}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]^{2}}{\left[\mathrm{H}_{2}\right]^{2}[\mathrm{NO}]^{2}}\)
At equilibrium \(\mathrm{r}_{\mathrm{f}}=\mathrm{r}_{\mathrm{b}}\)
\(\mathrm{k}_{\mathrm{f}}\left[\mathrm{H}_{2}\right][\mathrm{NO}]^{2}=\mathrm{k}_{\mathrm{b}} \frac{\left[\mathrm{N}_{2}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]^{2}}{\left[\mathrm{H}_{2}\right]}\)
Hence, rate expression for reverse reaction.
\(=\mathrm{k}_{\mathrm{b}} \frac{\left[\mathrm{N}_{2}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]^{2}}{\left[\mathrm{H}_{2}\right]}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionત્રણ પગલાની પ્રક્રિયા માટે ઉર્જાના આલેખની આકૃતિ દોરો જેમાં પ્રથમ પગલું સૌથી ધીમું અને છેલ્લું પગલું સૌથી ઝડપી છે. (ધારો કે પ્રકિયા ઉષ્માશોષક છે )
- 2$2O_3 \rightarrow 3O_2$ રાસાયણિક પ્રક્રિયા નીચે મુજબ દર્શાવી છે. તો દર નિયમ સમીકરણ..... થશે.View Solution
$ O_3 $ $\rightleftharpoons$ $ O_2 + O$ ...... (ઝડપી) ;
$O + O_3 \rightarrow 2O_2$ ...... (ધીમી)
- 3પ્રક્રિયા $A \to $ Products માં $A$ ની સાંદ્રતા મૂળ સાંદ્રતાની અડધી કરતા પ્રક્રિયાવેગ ચોથા ભાગનો થાય છે. તો પ્રક્રિયાનો કમ જણાવો.View Solution
- 4પ્રથમ ક્રમની પ્રક્રિયામાં પ્રક્રિયકની સાંદ્રતા $20$ મિનિટમાં $1.0\,M$ થી $0.25 \,M$ સુધી ઘટે છે. તો પ્રક્રિયાનો દર અચળાંક શું થશે?View Solution
- 5વાયુમય પ્રક્રિયા માટે, દર $= k [A] [B].$ જો પાત્રનું કદ ઘટીને $1/4$ પ્રારંભિક થશે તો પ્રક્રિયાનો દર પ્રારંભિક સમયમાં....... થશે.View Solution
- 6નીચેના વિશેષો માટે પ્રથમ ક્રમના તત્વો સાથે પ્રથમ વર્તુળ પ્રક્રિયા વિશેષોમાં માન્ય રેક્ટિવ હોય છે, જેમાં સ્થિર તાપમાન છે.View Solution
$\mathrm{A}+\mathrm{B} \underset{\text { Step } 3}{\text { Step } 1} \mathrm{C} \xrightarrow{\text { Step } 2} \mathrm{P}$
પ્રથમના વર્તુળ પ્રક્રિયાની માહિતી નીચે સૂચવેલી છે.
સ્ટેપ Rate constant $\left(\sec ^{-1}\right)$
Activation energy
$\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$
$1$ ${k}_1$ $300$ $2$ ${k}_2$ $200$ $3$ ${k}_3$ $\mathrm{Ea}_3$ ઉપરોક્ત રીતેની પ્રક્રિયાનું વધારણીક વર્તુળ $(k)$ આપવામાં આવે છે. $\mathrm{k}=\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_3}$ અને ઉપરોક્ત વધારણીક તાપ $(E_2)= 400$ કેલ્વિન છે, તો $\mathrm{Ea}_3$ નું મૂલ્ય છે $\mathrm{kJ} \mathrm{mol}^{-1}$ (નજીકની પૂર્ણાંક).
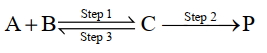
- 7$NaOH$ દ્વારા થતી સાબુની એસ્ટરીકરણ પ્રક્રિયાનો તાપમાન ગુણાંક $1.75$ છે. તો પ્રકિયાની સક્રિયકરણ ઊર્જા .......... $kcal\,mo{l^{ - 1}}$ થશે.View Solution
- 8$2X + Y \rightarrow Z + W,$ પ્રાથમિક પ્રક્રિયા માટે આણ્વીયતા.....View Solution
- 9$N_{2(g)} + 3H_{2(g)} \rightarrow 2NH_{3(g)}$ પ્રક્રિયા તાપમાનની ચોક્કસ પરિસ્થિતિ અને પ્રક્રિયકોનું આંશિક દબાણ હેઠળ થાય છે. $ NH_3$ નો નિર્માણ દર $ 0.001\,\,kg\, h^{-1}$ છે. તો $H_2$ નો રૂપાંતરણ દર તેજ સમાન પરિસ્થિતિમાં......$kg \,h^{-1}$ છે.View Solution
- 10નીચે આપેલ દર અચળાંક $(k)$ સાથે તાપમાન $(T)$ વચ્ચેનો તફાવત આલેખમાં દર્શાવ્યો છે. તો કયો આલેખ આર્હેંનિયસ સમીકરણનું પાલન કરે છે.View Solution