$NaOH$ દ્વારા થતી સાબુની એસ્ટરીકરણ પ્રક્રિયાનો તાપમાન ગુણાંક $1.75$ છે. તો પ્રકિયાની સક્રિયકરણ ઊર્જા .......... $kcal\,mo{l^{ - 1}}$ થશે.
Medium
Download our app for free and get started
a
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પ્રક્રિયાનો વેગ $r=K[x]\, [y]/[OH^-]$ છે. જો $[OH^-]$ વધારે હોય, તો પ્રક્રિયાકમ ........ થશે.View Solution
- 2$NO$ અને $Br_2$ વચ્ચેની પ્રક્રિયાથી $NOBr$ બનવાની પ્રક્રિયાની કાર્યપ્રણાલી નીચે મુજબ છે. :View Solution
$NO(g) + Br_2 (g) \rightleftharpoons NOBr_2 (g)$
$NOBr_2(g)+ NO(g)\longrightarrow 2NOBr(g)$
જો બીજો તબક્કો ધીમો તબક્કો હોય, તો $NO(g)$ ની સાપેક્ષે પ્રક્રિયા ક્રમ ........ થશે.
- 3પ્રથમ ક્રમની પ્રક્રિયા જે $30$ મિનિટમાં $30\%$ પૂર્ણ થાય છે તેનો અર્ધ આયુષ્ય સમયગાળો $.........$ મિનિટ થશે.View Solution
- 4નીચે બે વિધાન આપેલા છે :View Solution
વિધાન $I$ : $A+B \rightarrow C$ પ્રક્રિયા માટે વેગ નિયમ, વેગ $(r)=k[A]^2[B]$ છે. જ્યારે $A$ અને $B$ એમ બંને ની સાંદ્રતા બમણી કરવામાં આવે છે ત્યારે પ્રક્રિયા વેગ વધી ને " $x$ " ગણો થાય છે.
વિધાન $II$ :
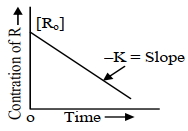
(Image)
આકૃતિ " " $y$ " ક્રમ પ્રક્રિયા માટે સાંદ્રતામાં તફ઼ાવત સામે સમયનો આલેખ દર્શાંવે છે. $x+y$ નું મૂલ્ય . . . . . છે.
- 5$975\, {~K}$ પર નીચે આપેલ રાસાયણિક પ્રક્રિયા માટે નીચેની માહિતી મેળવવામાં આવ્યો હતો.View Solution
$2 {NO}_{({g})}+2 {H}_{2({~g})} \rightarrow {N}_{2({~g})}+2 {H}_{2} {O}_{({g})}$
$[NO]$
${mol} {L}^{-1}$
${H}_{2}$
${mol} {L}^{-1}$
વેગ
${mol}L^{-1}$ $s^{-1}$
$(A)$ $8 \times 10^{-5}$ $8 \times 10^{-5}$ $7 \times 10^{-9}$ $(B)$ $24 \times 10^{-5}$ $8 \times 10^{-5}$ $2.1 \times 10^{-8}$ $(C)$ $24 \times 10^{-5}$ $32 \times 10^{-5}$ $8.4 \times 10^{-8}$ ${NO}$ના સંદર્ભમાં પ્રક્રિયાનો ક્રમ $....$ છે.
- 6પ્રથમ ક્રમની પ્રક્રિયા $A → B$ માટે દર અયળાંક $k =5.5 \times 10^{-14} s ^{-1} .67 \%$ પૂર્ણ થવા માટેનો જરૂરી સમય તેના પ્રક્રિયાના અર્ધ આયુષ્ય કરતા $x \times 10^{-1}$ ગણો છે. તો $x$ નું મૂલ્ય $\dots\dots$છે.View Solution
- 7પ્રથમ ક્રમ પ્રક્રિયા માટે, $75 \,\%$ પૂર્ણ થવા માટેનો સમય અને $50\, \%$ પૂર્ણ થવા માટેનો સમયનો ગુણોત્તર $....$ છે. (પૂર્ણાંકમાં જવાબ)View Solution
- 8ઉષ્માક્ષેપક પ્રક્રિયા $A\rightarrow B$ ની સક્રિયકરણ ઊર્જા $15\,\,K\,cal/mol$ છે અને પ્રક્રિયાની ઉષ્મા $5 \,\,K\,cal/mol$ છે. તો $B \rightarrow A $ પ્રક્રિયા માટેની સક્રિયકરણ ઊર્જા ......... $K\,cal/mol$ થશે.View Solution
- 9પ્રકિયા માટેView Solution
$2{N_2}{O_5}\, \to \,4N{O_2}\, + \,{O_2}$
પ્રકિયા નો દર શું હશે ?
- 10$X \rightarrow Y$ ઉષ્માશોષક પ્રક્રિયાને ધ્યાનમાં લેતાં પુરોગામી અને પ્રતિગામી પ્રક્રિયા માટેની સક્રિયકરણ ઊર્જા અનુક્રમે $E_b $ અને $E_f $ છે. તો સામાન્ય રીતે.View Solution