પ્રક્રિયા,
(Image)
નીચે આપેલા ક્યા ગેલ્વેનિક કોષમાં થાય છે ?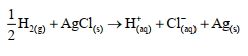
JEE MAIN 2024, Medium
Download our app for free and get started
c
Anodic half cell
Anodic half cell
Gas - gas $1$on electrode
$\frac{1}{2} \mathrm{H}_{2(\mathrm{~g})} \rightarrow \mathrm{H}_{(\mathrm{aq})}^{+}+\mathrm{e}^{-}$
Cathodic Reaction
Metal-metal insoluble salt anion electrode
$\mathrm{Ag}_{(\mathrm{aq})}^{+}+\mathrm{e}^{-} \rightarrow \mathrm{Ag}_{(\mathrm{s})}$
$\mathrm{AgCl}_{(\mathrm{s})} \rightleftharpoons \mathrm{Ag}_{(\mathrm{aq})}^{+}+\mathrm{Cl}_{(\mathrm{aq})}^{-}$
$\mathrm{AgCl}_{(5)}+\mathrm{e}^{-} \rightarrow \mathrm{Ag}_{(\mathrm{s})}+\mathrm{Cl}_{(\mathrm{aq})}^{-}$
Overall redox reaction
$\frac{1}{2} \mathrm{H}_{2(\mathrm{~g})}+\mathrm{AgCl}_{(\mathrm{s})} \rightarrow \mathrm{H}_{(\mathrm{sq})}^{+}+\mathrm{Cl}_{(\mathrm{aq})}^{-}+\mathrm{Ag}_{(\mathrm{s})}$
Cell Representation
$\mathrm{Pt}\left|\mathrm{H}_{2(\mathrm{~g})}\right| \mathrm{kCl}_{(\mathrm{sol})}\left|\mathrm{AgCl}_{(\mathrm{s})}\right| \mathrm{Ag}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઔદ્યોગિક ઉત્પાદનમાં વિદ્યુત વિભાજનથી બે કલાકમાં $40$ કિ.ગ્રા. કેલ્શિયમ મળે છે. બે કલાક માટે આટલો જ પ્રવાહ પસાર કરતા કેટલા ............ $\mathrm{kg}$ એલ્યુમિનિયમ ઉત્પન્ન થાય? ($Ca$ નો પ.ભા.$= 40,\, Al = 27$)View Solution
- 2View Solutionપ્રમાણિત હાઈડ્રોજન ધ્રુવ એ શૂન્ય ધ્રુવ પોટેન્શિયલ ધરાવે છે કારણ કે. .....
- 3$298\,K$ પર, $Cu ^{2+} / Cu$ ઈલેકટ્રોડ માટે પ્રમાણિત રિડકશન પોટેન્શિયલ $0.34\,V$ છે.આપેલ : $K _{ sp } Cu ( OH )_2=1 \times 10^{-20}$ $\operatorname{Take} \frac{2.303 RT }{ F }=0.059 \,V$ લો.ઉપરના કપલ (યુગ્મ) માટે $pH =14$ પર રિડકશન પોટેન્શિયલ $(-) x \times 10^{-2}\,V$ છે.$x$નું મુલ્ય $........$ છે.View Solution
- 4આપેલ પ્રક્રિયાView Solution
$Cu(s) + 2Ag{^+}_{(aq)} \to Cu^{+2}_{(aq)} + 2Ag(s)$
માટે સંતુલન અચળાંક $K_C = 10 \times 10^{15}$ છે, તો $298\, K$ ને $E_{cell}^o$ નું મૂલ્ય કેટલુ થશે?
[${2.303\,\frac{{RT}}{F}}$ એ $298\,K$ $=0.059\,V$]
- 5જો કોષમાં $0.01 \,M$ વિદ્યુત વિભાજ્યનો અવરોધ $40$ ઓહ્મ છે. કોષ અચળાંક $0.4$ સેમી$^{-1}$ છે. તો તેમની મોલર વાહકતા ઓહ્મ$^{-1}$ સેમી$^{2}$ મોલ$^{-1}$ માં કેટલી થાય?View Solution
- 6ત્રણ ધાતુઓ $A, B $ અને$ C$ પ્રમાણિત રીડક્શન પોટેન્શિયલ અનુક્રમે $+ 0.5\, V, -3.0 \,V$ અને $-1.2\,V$ છે. આ ધાતુઓનો રીડ્યુસીંગ શક્તિનો ક્રમ એ કયો છે?View Solution
- 7View Solutionસાચું વિધાન ઓળખો.
- 8$M^{3+}/M$ વિદ્યુતધ્રુવનો પ્રમાણિત પોટેન્શિયલ શોધવા માટે નીચેનો કોષ રચાયો છે:View Solution
$Pt/ M/M^{3+}(0.001 \,mol\, L^{ -1})/Ag^+(0.01\, mol\, L^{-1})/Ag$
$298\, K$ પર સેલનો $emf$ $0.421\, volt$ હોવાનું જાણવા મળ્યું છે. $298\, K$ પર અર્ધ પ્રક્રિયા $M^{3+} + 3e \to M$ નો પ્રમાણિત પોટેન્શિયલ ......... $\mathrm{volt}$ હશે .
(આપેલ છે: $298\, K$ પર $E_{A{g^ + }/Ag}^o \,=\, 0.80\, Volt$ )
- 9$288K\, AgCl$ નાં સંતૃપ્ત દ્રાવણની વાહકતા $1.382 × 10^{-6}$ ઓહ્મ $^{-1}$ સે.મી$^{-1}$ મોલ$^{-1}$ છે. તેમની દ્રાવ્યતા $gL^{-1}$ શોધો. અનંત મંદને $Ag^{+}$ અને $Cl^{-}$ ની આયોનિક વાહકતા અનુક્રમે $61.9$ ઓહ્મ$^{-1}$ સે.મી$^{2}$ મોલ$^{-1}$ અને $76.3 $ ઓહ્મ$^{-1}$ સે.મી$^{2}$ મોલ$^{-1}$ છે.View Solution
- 10$2[Fe(CN)6]^{-3} + H_2O_2 + 2OH- \rightarrow 2[Fe(CN)_6]^{4-} + 2H_2O + O_2$ પ્રક્રિયામાં રીડકટન્ટનો તુલ્યભાર શું થશે ?$( Fe = 56, C = 12, N = 14, O = 16, H = 1)$View Solution