પ્રક્રિયકની સાંદ્રતા $0.5\, M$ હોય ત્યારે પ્રથમ ક્રમની એક પ્રક્રિયાનો વેગ $1.5 \times 10^{-2}$ મોલ$^{-1}$ મિનિટ$^{-1}$ છે. તો પ્રક્રિયાનો અર્ધઆયુષ્ય સમય .......... મિનિટ છે.
AIPMT 2004, Medium
Download our app for free and get started
d
(d) Rate $\left( {\frac{{dx}}{{dt}}} \right) = K.c$ ;
(d) Rate $\left( {\frac{{dx}}{{dt}}} \right) = K.c$ ;
$1.5 \times {10^{ - 2}} = K \times 0.5$
For first order
$K = \frac{{1.5 \times {{10}^{ - 2}}}}{{0.5}} = 3 \times {10^{ - 2}}\min^{ - 1}$
${t_{1/2}} = \frac{{0.693}}{K} = \frac{{0.693}}{{3 \times {{10}^{ - 2}}}} = 23.1\;\min$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$Kt = lnC_0 - lnC_t$ સમીકરણમાં $ t$ અને $lnC_t$ વચ્ચેનો વક્ર ..... માં હોય.View Solution
- 2જો $ t_{1/2} 20$ મિનિટ હોય તો $10 $ મિનિટ પછી પ્રથમ ક્રમની પ્રક્રિયકનો આંશિક ભાગ કેટલો?View Solution
- 3ક્લોરિન પરમાણુઓની હાજરીમાં ઓઝોનની ઓકિસજન પરમાણુઓ સાથેની પ્રક્રિયા નીચે દર્શાવેલ બે તબક્કા મુજબ થઈ શકે છે.View Solution
${O_3}(g)\, + \,C{l^ * }(g)\, \to \,{O_2}(g) + Cl{O^ * }(g)$ ..... $(i)$ $[{K_i} = 5.2 \times {10^9}\,\,L\,mo{l^{ - 1}}\,{s^{ - 1}}]$
$Cl{O^ * }(g) + {O^ * }(g)\, \to \,{O_2}(g) + \,C{l^ * }(g)$ ..... $(ii)$ $[{K_{ii}} = 2.6 \times {10^{10}}\,\,L\,mo{l^{ - 1}}\,{s^{ - 1}}]$
તો સમગ્ર પ્રક્રિયા ${O_3}(g){\mkern 1mu} + {\mkern 1mu} {O^*}(g){\mkern 1mu} \to {\mkern 1mu} 2{O_2}(g)$ માટે સમગ્ર પ્રક્રિયાનો વેગ .......... $L\,\,mo{l^{ - 1}}\,{s^{ - 1}}$ અચળાંક કોની સૌથી નજીક હશે ?
- 4કાર્બનિક ક્લોરાઇડનું જળવિભાજન વધુ પ્રમાણમાં પાણીની હાજરીમાં નીચે પ્રમાણે કરવામાં આવે છે. $R - Cl + H_2O \rightarrow R - OH + HCl $ તો નીચેના પૈકી કયો વિકલ્પ સાચો છે ?View Solution
- 5પ્રથમ ક્રમની પ્રક્રિયા $A \rightarrow$ નીપજો માટે $A$ ની સાંદ્રતા $0.1\, M$ થી $0.025\, M$ થવા $40$ મિનિટનો સમય લાગે છે. તો જ્યારે $A$ ની સાંદ્રતા $0.01\, M$ હોય ત્યારે પ્રક્રિયાનો વેગ............$\times 10^{-4}\,M/ \min$ થશે.View Solution
- 6$\log(a - x)$ વિરૂદ્ધ સમય $t$ નો આલેખ સીધી રેખામાં છે જે દર્શાવે છે કે પ્રક્રિયા ....... ક્રમની છે.View Solution
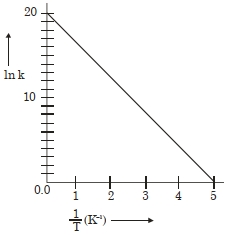
- 7એક પ્રક્રિયા માટે, $\ln K$ વિરુદ્ધ $\frac{1}{ T }$ નો આલેખ નીચે આપેલો છે. પ્રક્રિયાની સક્રિયકરણ ઊર્જા $......cal$ $mol ^{-1}$ (નજીકના પૂર્ણાંક)View Solution
(આપેલું છે: $R =2\,cal\,K ^{-1}\,mol ^{-1}$ )
- 8એક પ્રક્રિયા માટે જરૂરી $NO_2$ એ $CCl_4$ માં $N_2O_5$ ના નીચેના સમીકરણ મુજબના વિઘટનથી મળે છે.View Solution
$2N_2O_5 (g) \to 4NO_2 (g) + O_2 (g)$
$N_2O_5$ ની શરૂઆતની સાંદ્રતા $3.00\, mol\, L^{-1}$ છે. અને $30$ મિનિટ બાદ તે $2.75\, mol\, L^{-1}$ છે. તો $NO_2$ તા સર્જનનો દર ................ $mol\, L^{-1}\, min^{-1}$ જણાવો.
- 9$100\,^oC$ તાપમાને પ્રથમ ક્રમની એક પ્રક્રિયાનો વેગ અચળાંક $K= 1.5 \times 10^{-2}\,s^{-1}$ છે. જો પ્રકિયકની શરૂઆતની સાંદ્રતા $100\, mol\,L^{-1}$ હોય, તો $10\,\min$ પછી પ્રક્રિયકની સાંદ્રતા કેટલી થશે ?View Solution
- 10પદાર્થ $A$ અને $B$ વચ્ચેની પ્રક્રિયા માટેની વેગનિયામ નીચે મુજબ છે. વેગ $= K[A]^n[B]^m $ જો $A$ નું સાંદ્રણ બમણું કરવામાં આવે તથા $B$ ની સાંદ્રતા અડધી કરવામાં આવે તો નવા વેગ એ મૂળવેગ વચ્ચેનો ગુણોત્તર કેટલો થશે ?View Solution