જો $ t_{1/2} 20$ મિનિટ હોય તો $10 $ મિનિટ પછી પ્રથમ ક્રમની પ્રક્રિયકનો આંશિક ભાગ કેટલો?
Diffcult
Download our app for free and get started
a
$K\, = \,\,\frac{{0.693}}{{{t_{1/2}}}}\,\, = \,\,\frac{{0.693}}{{20}}$
$K\, = \,\,\frac{{0.693}}{{{t_{1/2}}}}\,\, = \,\,\frac{{0.693}}{{20}}$
$K\,\, = \,\,\frac{{2.303}}{t}\,\log \,\frac{a}{{(a\, - \,x)}}\,\,\,\, \Rightarrow \,\,\,\frac{{0.693}}{{20}}\,\, = \,\,\frac{{2.303}}{{40}}\,\log \,\frac{a}{{(a\, - \,x)}}$
$2\,\, \times \,\,0.3010\,\, = \,\,\log \,\frac{a}{{(a\, - x)}}\,\,\,\, \Rightarrow \,\,\,2\,\, \times \,\,\log \,2\,\, = \,\,\log \frac{a}{{(a\, - \,x)}}$
$\log \,\,{2^2}\, = \,\,\log \frac{a}{{(a\, - \,x)}}\,\,\,\, \Rightarrow \,\,\,\frac{a}{{(a\, - \,x)}}\,\, = \,\,4\,\,\,\, \Rightarrow \,\,\,\,\frac{{a\, - \,\,x}}{a}\,\, = \,\,\frac{1}{4}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$Kt = lnC_0 - lnC_t$ સમીકરણમાં $ t$ અને $lnC_t$ વચ્ચેનો વક્ર ..... માં હોય.View Solution
- 2$25^{\circ} C$ પર $3.33\, h$ અર્ધ-આયુષ્ય સાથે, સુક્રોઝ એસિડ દ્રાવણમાં ગ્લૂકોઝ અને ફ્રૂકટોઝમાં જળવિભાજન પામે છે જે પ્રથમ ક્રમ વેગ નિયમને અનુસરે છે. $9\, h$ પછી, સુક્રોઝનો અંશ $f$ બાકી રહે છે. તો $\log _{10}\left(\frac{1}{f}\right)$ નું મૂલ્ય ..... $\times 10^{-2}$ છે.View Solution
(નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ) (ધારી લો : $\ln 10=2.303, \ln 2=0.693$)
- 3એક કાર્બનિક પદાર્થનું પ્રથમ ક્રમ હેઠળ વિધટન થાય છે. $60 \%$ વિધટન માટે લાગતો સમય $90 \%$ હોય તો, $540\,s$ વિઘટન માટે જરૂરી સમય $..........s$ હશે.(નજીકનો પૂર્ણાંક)(આપેલ : $\ln 10=2.3 ; \log 2=0.3$ )View Solution
- 4પદાર્થ $A $ અને $B$ વચ્ચેનો પ્રક્રિયા દર સમીકરણ દર $= k[A]^n[B]^m$ આપેલ છે. જો $A$ ની સાંદ્રતા બમણી અને $B$ ની સાંદ્રતા શરૂઆતની સાંદ્રતાથી અડધી થાય તો પહેલાનાં દર કરતાં હાલનો દર ગુણોત્તર ... થાય.View Solution
- 5View Solutionઅસરકારક અથડામણ માટે અથડામણ સમયે પ્રક્રિયક અણુઓ પાસે જે ન્યૂનતમ ઊર્જા હોવી જોઇએ તેને ... કહે છે.
- 6$2N_2O_5(g) \rightarrow 4NO_2(g) + O_2(g)$ પ્રક્રિયા $N_2O_5 $ ના સંદર્ભમાં પ્રથમ ક્રમની છે તો નીચેનામાંથી કયો આલેખ સીધે રેખામાં મળે છે?View Solution
- 7પ્રક્રિયા $2FeC{l_3} + SnC{l_2} \to 2FeC{l_2} + SnC{l_4}$ શેનું ઉદાહરણ છે?View Solution
- 8મોટા ભાગની પ્રક્રિયાનો તાપમાન ગુણાંક $.......$ ની વચ્ચે હોય છે.View Solution
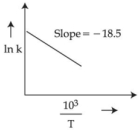
- 9$700 -$ $1000\,K$ તાપમાન શ્રેણીમાં (વિસ્તાર માં) એસિટાલ્ડીહાઈડના વિઘટન માટેના દર (વેગ) અચળાંક માપવામાં આવ્યાં. $\ln k$ વિરુદ્ધ $\frac{10^{3}}{ T }$ આલેખ દોરીને માહિતીનું પૃથ્થકરણ કરવામાં આવ્યું.પ્રક્રિયા માટે સક્રિયકરણ શક્તિનું મૂલ્ય $\dots\dots\dots$$kJ\,mol { }^{-1}$ છે.(નજીકનો પૂર્ણાંક)View Solution
(આપેલ:$R =8.31\,JK ^{-1}\,mol ^{-1}$)
- 10પ્રક્રિયા માટેનો દર સતત $\underline{a}$ દ્વારા વધારી શકાય છે પ્રકીયક ની સ્થિરતા અથવા $\underline{b}$ સંક્રમણ સ્થિતિની સ્થિરતા. $a$ અને $b$ માટે યોગ્ય પસંદગી પસંદ કરોView Solution