Let internal resistance of source \(=\mathrm{R}\)
Current in coil of resistance
\(\mathrm{R}_{1}=\mathrm{I}_{1}=\frac{\mathrm{V}}{\mathrm{R}+\mathrm{R}_{1}}\)
Current in coil of resistance
\(\mathrm{R}_{2}=\mathrm{I}_{2}=\frac{\mathrm{V}}{\mathrm{R}+\mathrm{R}_{2}}\)
Further, as heat generated is same, so
\(\mathrm{I}_{1}^{2} \mathrm{R}_{1} \mathrm{t}=\mathrm{I}_{2}^{2} \mathrm{R}_{2} \mathrm{t}\)
or \(\quad\left(\frac{\mathrm{V}}{\mathrm{R}+\mathrm{R}_{1}}\right)^{2} \mathrm{R}_{1}=\left(\frac{\mathrm{V}}{\mathrm{R}+\mathrm{R}_{2}}\right)^{2} \mathrm{R}_{2}\)
\(\Rightarrow \quad \mathrm{R}_{1}\left(\mathrm{R}+\mathrm{R}_{2}\right)^{2}=\mathrm{R}_{2}\left(\mathrm{R}+\mathrm{R}_{1}\right)^{2}\)
\(\Rightarrow \mathrm{R}^{2} \mathrm{R}_{1}+\mathrm{R}_{1} \mathrm{R}_{2}^{2}+2 \mathrm{RR}_{1} \mathrm{R}_{2}\)
\(\Rightarrow \quad \mathrm{R}^{2} \mathrm{R}_{2}+\mathrm{R}_{1}^{2} \mathrm{R}_{2}+2 \mathrm{RR}_{1} \mathrm{R}_{2} ?\)
\(\Rightarrow \quad \mathrm{R}^{2}\left(\mathrm{R}_{1}-\mathrm{R}_{2}\right)=\mathrm{R}_{1} \mathrm{R}_{2}\left(\mathrm{R}_{1}-\mathrm{R}_{2}\right)\)
\(\Rightarrow \quad \mathrm{R}=\sqrt{\mathrm{R}_{1} \mathrm{R}_{2}}\)
Download our appand get started for free
Similar Questions
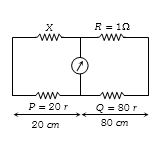
- 1આપેલ પરિપથમાં એમીટરમાથી પ્રવાહ પસાર ના થતો હોય તો $X$ નું કેટલા ............... $\Omega$ હશે?View Solution
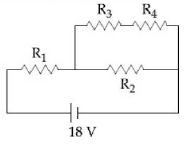
- 2આપેલ પરિપથમાં $18\ V$ કોષનો આંતરિક અવરોધ અવગણ્ય છે. જો $R_1 = 400\,\Omega , R_3 = 100\, \Omega$ અને $R_4 = 500\,\Omega$, અને જો $R_4$, ની સાપેક્ષે આદર્શ વોલ્ટમીટરનું વાંચન $5\, V$ છે, તો $R_2$ નું મૂલ્ય કેટલા ................ $\Omega$ હશે.View Solution
- 3$E_1$ અને $E_2$ $e.m.f.$ ના બે કોષોને શ્રેણીમાં જોડેલા છે.અને પોટેન્શીયોમીટરના તારની બેલેન્સીંગ લંબાઈ $625\,cm$ છે.જો $E_1$ ના ટર્મીનલને બદલવામાં આવે, તો મેળવેલી બેલેન્સીંગ લંબાઈ $125\,cm$ છે.આપેલ છે કે $E_2 > E_1$ તો $E_1: E_2$ ના ગુણોતર શું હોય શકે?View Solution
- 4$5\,A$ ના ફ્યુઝનો ઉપયોગ કરીને $220\,V$ પર $60\,W$ બલ્બ સલામત રીતે ચલાવી શકાય?View Solution
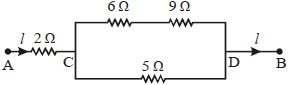
- 5પરિપથમાં $5\,\Omega $માં પ્રવાહ પસારના કારણે ઉત્પન્ન થતી ઉષ્મા $20.00\,cal/s$ છે, તો $2\,\Omega$ અવરોધમાં ઉત્પન્ન થતી ઉષ્મા $....... cal/s$View Solution
- 6$l$ લંબાઈ અને $r$ ત્રિજ્યા ધરાવતા તારનો અવરોધ $100\, \Omega $ છે.તેને ઓગળીને નવો $\frac{r}{2}$ ત્રિજ્યાનો તાર બનાવવામાં આવે તો નવા તારનો અવરોધ કેટલા ............... $\Omega$ થશે?View Solution
- 7આંતરિક અવરોધ $r$ ધરાવતી બેટરી સાથે $R$ અવરોધ જોડેલ છે $R$ અવરોધ પર મહત્તમ પાવર કરવા માટે ...View Solution
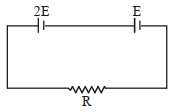
- 8$2\, E$ અને $E$ કોષના આંતરિક અવરોધ અનુક્રમે $r _{1}$ અને $r _{2}$ છે જે આકૃતિમાં દર્શાવ્યા પ્રમાણે બાહ્ય અવરોધ $R$ સાથે જોડેલ છે. $R$ ના કયા મૂલ્ય માટે પ્રથમ કોષનો ટર્મિનલ વૉલ્ટેજ શૂન્ય થાય?View Solution
- 9પોટેન્શિયોમીટર દ્વારા બે કોષને શ્રેણીમાં સહાયકમાં જોડતાં તટસ્થ બિંદુ $6\, m$ અને બે કોષને શ્રેણીમાં વિરોધકમાં જોડતાં તટસ્થ બિંદુ $2\, m $ અંતરે મળે છે.તો બંને કોષનાં $emf$ નો ગુણોત્તર કેટલો થાય?View Solution
- 10એક મકાનમાં $45\; \mathrm{W}$ ના $15$ બલ્બ, $100\; \mathrm{W}$ ના $15$ બલ્બ, $10\; \mathrm{W}$ ના $15$ નાના પંખા અને $1 \;\mathrm{kW}$ના $2$ હીટર છે.મુખ્ય ઈલેક્ટ્રિક તારનો વૉલ્ટેજ $220\; \mathrm{V}$ હોય તો મકાનની ન્યુનત્તમ ફ્યુજ ક્ષમતા કેટલા ............... $A$ હોવી જોઈએ?View Solution
