પૃથ્વીની સપાટીથી કેટલી ઊંચાઈ $h$ માટે ગુરુત્વ પ્રવેગ પૃથ્વીની સપાટીથી $h$ ઊંડાઈ જેટલો થાય. પૃથ્વીની ત્રિજ્યા $r$ અને પૃથ્વીના ભ્રમણની અસર અવગણો.
JEE MAIN 2020, Diffcult
a
\(M =\) mass of earth
\(M =\) mass of earth
\(M _{1}= mass\) of shaded portion
\(R =\) Radius of earth
\(M_{1}=\frac{M}{\frac{4}{3} \pi R^{3}} \cdot \frac{4}{3} \pi(R-h)^{3}\)
\(=\frac{M(R-h)^{3}}{R}\)
Weight of body is same at \(P\) and \(Q\)
i.e. \(mg _{ P }= mg _{ Q }\)
\(g _{ P }= g _{ Q }\)
\(\frac{G M_{1}}{(R-h)^{2}}=\frac{G M}{(R+h)^{2}}\)
\(\frac{G M(R-h)^{3}}{(R-h)^{2} R^{3}}=\frac{G M}{(R+h)^{2}}\)
\(( R - h )( R + h )^{2}= R ^{3}\)
\(R^{3}-h R^{2}-h^{2} R-h^{3}+2 R^{2} h-2 R h^{2}=R^{3}\)
\(R^{2}-R h^{2}-h^{3}=0\)
\(R^{2}-R h-h^{2}=0\)
\(h ^{2}+ Rh - R ^{2}=0 \Rightarrow h =\frac{- R \pm \sqrt{ R ^{2}+4 R ^{2}}}{2}\)
ie \(h =\frac{- R +\sqrt{5} R }{2}=\left(\frac{\sqrt{5}-1}{2}\right) R\)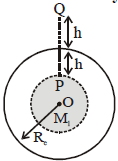
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે પદાર્થ જેનું દળ $m_1$ અને $m_2$ છે તે અનંત અંતરે સ્થિર પડેલા છે. હવે તે બંને એકબીજા તરફ ગુરુત્વાકર્ષણ બળને લીધે ગતિ કરે છે. જ્યારે તે બંને એકબીજાથી $r$ અંતરે આવે ત્યારે તેનો સાપેક્ષ વેગ કેટલો થાય ?View Solution
- 2$M$ દળ અને $R$ ત્રિજ્યા ધરાવતી પૃથ્નીની સપાટી ઉપરથી, સપાટીથી $2 R$ ઉંચાઈએ વર્તુળાકાર કક્ષામાં $m$ દળ ધરાવતા ઉ૫ગ્રહને તરતો મૂક્વા માટે જરૂરી લધુતમ ઊર્જા. . . . . . . . છે.View Solution
- 3$m$ અને $M$ દળ ધરાવતા બે ગોળા હવામાં છે અને તેમની વચ્ચે લાગતું ગુરુત્વાકર્ષણ બળ $F$ છે. દળોની વચ્ચે જગ્યામાં $3$ વિશિષ્ટ ઘનતા ઘરાવતું પ્રવાહી ભરવામાં આવે છે. હવે, ગુરુત્વાકર્ષણ બળ કેટલું થાય?View Solution
- 4એક સ્થાને ગુરુત્વ પ્રવેગ નું મૂલ્ય $9.8\; m/s^2$ જો પૃથ્વી સંકોચાય ને તેના પરિમાણ થી અડધી થય જાય પણ દળ સમાન રહે તો ગુરુત્વ પ્રવેગનું મૂલ્ય ........ $m/{\sec ^2}$ થશે.View Solution
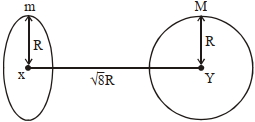
- 5આકૃતિમાં દર્શાવેલ ગોળા અને વલય (રીંગ) વચ્ચે આકર્ષણ બળ શોધો, જ્યાં રીંગનું સમતલ કેન્દ્રોને જોડતી રેખાને લંબરૂપે છે. બે રિંગ $('m'$ દળ) નાં કેન્દ્ર થી ગોળા $('M'$ દળ)નાં કેન્દ્ર વચ્ચેનું અંતર $\sqrt{8} R$ હોય તેમજ બંને એકસરખી ત્રિજ્યા $'R’$ ધરાવે છે.View Solution
- 6પૃથ્વીના કેન્દ્રથી અંતર $d$ સાથે ગુરુત્વપ્રવેગ $g$ માં થતા બદલાવને શ્રેષ્ઠ રીતે રજુ કરે છે. ($ R=$ પૃથ્વીની ત્રિજયા)View Solution
- 7પૃથ્વીની સપાટી પર પદાર્થનું વજન $72 \,N$ છે. જો તેને $h=2 R$ ઊંચાઈ એ લઈ જવામાં આવે, તો તેનું વજન ........... $N$ હશે ?View Solution
- 8View Solutionઉપગ્રહમાં એક ખુરશી પર બેઠેલો માણસ વજનરહિત હોય તેનું કારણ નીચેનામાથી શું હોય .
- 9એક ઉલ્કા પૃથ્વીના કેન્દ્ર તરફ ગતિ કરે છે. જ્યારે તે પૃથ્વીના કેન્દ્રથી $10 \mathrm{R}$ ($R$ પૃથ્વીની ત્રિજ્યા) અંતરે હોય ત્યારે તેનો વેગ $12 \;\mathrm{km} / \mathrm{s}$ છે.પૃથ્વીના વાતાવરણની અસરને અવગણતા ઉલ્કા પૃથ્વીની સપાટી પર કેટલા વેગથી ($km/s$ માં) પડશે? (પૃથ્વીની નિષ્ક્રમણ ઝડપ$=11.2 \;\mathrm{km} / \mathrm{s}$ )View Solution
- 10કેટલી ઊંડાઈ પર ગુરુત્વપ્રવેગ પૃથ્વીની સપાટી પરના ગુરુત્વપ્રવેગથી $\frac{1}{n}$ ગણો થાય ? (પૃથ્વીની ત્રિજ્યા $=R$ )View Solution
