$R$ અને $2R$ ત્રિજયાના નળાકાર સમઅક્ષીય મૂકેલા છે.તેમની ઉષ્મા વાહકતા $K_1$ અને $K_2$ છે,તો સમતુલ્ય ઉષ્મા વાહકતા શોધો.
IIT 1988, Medium
c
(c) Both the cylinders are in parallel, for the heat flow from one end as shown.
(c) Both the cylinders are in parallel, for the heat flow from one end as shown.
Hence \({K_{eq}} = \frac{{{K_1}{A_1} + {K_2}{A_2}}}{{{A_1} + {A_2}}}\); where \(A_1\)
= Area of cross-section of inner cylinder = \(\pi\) \(R_2\) and \({A_2} = \)Area of cross-section of cylindrical shell \( = \pi \{ {(2R)^2} - {(R)^2}\} = 3\pi {R^2}\)
\(\Rightarrow {K_{eq}} = \frac{{{K_1}(\pi {R^2}) + {K_2}(3\pi {R^2})}}{{\pi {R^2} + 3\pi {R^2}}} = \frac{{{K_1} + 3{K_2}}}{4}\)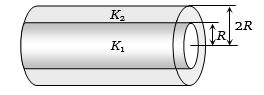
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ત્રણ જુદા જુદા તારાઓ $P, Q$ અને $R$ ના પ્રકાશના અભ્યાસ પરથી જાણવા મળ્યું કે પ્રકાશના $P$ ના વર્ણપટમાં જાંબલી રંગની તીવ્રતા મહત્તમ, $R$ ના વર્ણપટમાં લીલા રંગની તીવ્રતા મહત્તમ અને $Q$ ના વર્ણપટમાં લાલ રંગની તીવ્રતા મહત્તમ છે. જો $P, Q$ અને $R$ ના નિરપેક્ષ તાપમાન અનુક્રમે $T_P , T_Q$ અને $T_R$ હોય, તો ઉપરોક્ત અવલોકનો પરથી તે તારણ કાઢી શકાય છે કેView Solution
- 2View Solutionવિધાન : ટ્યુબલાઇટ સફેદ પ્રકાશ ઉત્સર્જિત કરે.
કારણ : ટ્યુબલાઇટમાં પ્રકાશનું ઉત્સર્જન ખૂબ ઊંચા તાપમાને થાય છે.
- 3ઉષ્મીય રીતે અલગ કરેલા એક સળિયાનાં બંને છેડાનાં તાપમાનો અનુક્રમે $T _{1}$ અને $T _{2}$ છે. સળિયો $l_{1}$ અને $l_{2}$ એમ બે વિભાગોના જોડાણથી બનેલો છે. બંને દ્રવ્યોની ઉષ્માવાહકતા $k _{1}$ અને $k _{2}$ છે. તો બે ભાગોની જોડતી સપાટીએ તાપમાન કેટલું થાય?View Solution

- 4સ્થાયી ઉષ્મા અવસ્થામાં રહેલો ધાતુનો સળિયો તેના એક છેડેથી બીજા છેડે ઉષ્માનું વહન કરે છે. સળિયાના ગરમ છેડાથી $x$ લંબાઈ મુજબ તેના તાપમાન $\theta$ માં થતા ફેરફરરનો આલેખ નીચેનામાંથી કેવો હશે?View Solution
- 5બે ગોળાઓની ત્રિજ્યાનો ગુણોત્તર $1:2$ અને ઘનતાનો ગુણોત્તર $2:1$ છે અને તેની વિશિષ્ટ ઉષ્મા સમાન છે. તેમને સમાન તાપમાને ગરમ કરી સમાન પરિસરમાં મુકવામાં આવે ત્યારે તાપમાનના ઘટાડાનો ગુણોત્તર ....થશે.View Solution
- 6$3000\,K$ તાપમાને રહેલ ફર્નેસ $1$ કલાકમાં એકમ ક્ષેત્રફળ દીઠ કેટલી ઉષ્મા વિકેરિત કરે? $( \sigma = 5. 7 \times 10^{-8}\,W\,m^{-2}\,K^{-4})$View Solution
- 7એક પાતળા ધાતુના કવચની ત્રીજ્યા $r$ અને તાપમાન $T$ જેટલું ગરમ કરવામાં આવે છે અને પછી ઠંડુ પાડવામાં આવે છે. કવચના ઠંડા પડવાનો દર કોના સમપ્રમાણમાં હશે?View Solution
- 8બે સમાન બોલ $A$ અને $B$ ને ગરમ કરતાં $A$ વાદળી અને $B$ લાલ દેખાય છે. તેમના તાપમાન વચ્ચેનો સંબંધ .....થશે.View Solution
- 9$ {r_1} $ અને $ {r_2} $ ત્રિજયા ધરાવતા સમાન દ્રવ્યના ગોળાના સપાટીના તાપમાન $ {T_1} $ અને $ {T_2} $ છે.જો તેનો ઉત્સર્જન પાવર સમાન હોય,તો ત્રિજયાનો ગુણોત્તર કેટલો થાય?View Solution
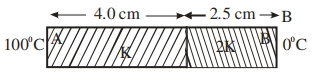
- 10આપેલ આકૃતિ અનુસાર, $K$ અને $2K$ જેટલી ઉષ્મીય વાહક્તા ધરાવતી બે તક્તિઓ $A$ અને $B$ ને એકસાથે જોડી એક સંયુક્ત તક્તિ બનાવવામાં આવે છે. તક્તિઓની જાડાઈ અનુક્રમે $4.0 \,cm$ અને $2.5 \,cm$ અને દરેેક તક્તિના આડછેદનું ક્ષેત્રફળ $120 \,cm ^{2}$ છે. સંયુક્ત તક્તિની સમતુલ્ય ઉષ્મીય વાહક્ત $\left(1+\frac{5}{\alpha}\right) K$ છે. તો $\alpha$ નું મૂલ્ય ............... થશે.View Solution