$R$ જેટલી ત્રિજ્યાં અને $m$ જેટલું દળ ધરાવતી પાતળી વિંટી તેનાં પરિધના એક નિશ્ચિત બિંદુ ઊર્ધ્વતલમાં લટકાવેલી છે. તેનાં દોલનોનો આવર્તકાળ કેટલો થશે ?
Medium
a
(a)
(a)
The time period of the disc is \(2 \pi \sqrt{(3 r / 2 g )}\)
We know that the time period of an object,
\(T =2 \pi \sqrt{(I / mgL )}\)
where,
\(I=\) moment of inertia from the suspended point
\(L =\) distance of its centre from suspended point \(= r\)
we know that, the moment of inertia of disc about its centre \(= mr ^2 / 2\)
using parallel axis theoram the moment of inertia from a point in its periphery,
\(I = mr ^2+ mr ^2 / 2=3 mr ^2 / 2\)
putting the values in the above equation we get,
\(2 \pi \sqrt{\left(3 mr ^2 / 2 mgr \right)}\)
\(=2 \pi \sqrt{(3 r / 2 g )}\)
therefore, the time period of the disc is \(2 \pi \sqrt{(3 r / 2 g )}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમતોલન સ્થાન પાસેથી સરળ આવર્ત ગતિ શરૂ કરતાં કણને આકૃતિમાં દર્શાવેલો છે. તેનો કંપવિસ્તાર $A$ અને આવર્તકાળ $T$ છે. કોઈ સમયે તેની ઝડપ મહત્તમ ઝડપથી અડધી થાય છે. તેનું સ્થાનાંતર કેટલું હશે?View Solution
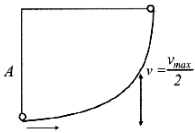
- 2સ.આ.ગ. કરતાં કણનો કંપવિસ્તાર $3\,cm$ છે. સ્થાનાંતર ($cm$ માં) કે જ્યાં તેની ગતિઊર્જા સ્થિતિઉર્જા કરતાં $25 \%$ વધુ હશે?View Solution
- 3k બળ અચળાંક ધરાવતી સ્પ્રિગ સાથે દળ $m$ જોડવામાં આવેલ છે અને તે મુજબ સપાટી જોડેલ છે.અને તે આકૃતિ મુજબ સપાટી જોડેલ બીજી સ્પ્રિંગને અડે છે. નાના દોલનોનો આવર્તકાળ કેટલો થાય?View Solution
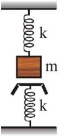
- 4$R$ જેટલી ત્રિજ્યાં અને $m$ જેટલું દળ ધરાવતી પાતળી વિંટી તેનાં પરિધના એક નિશ્ચિત બિંદુ ઊર્ધ્વતલમાં લટકાવેલી છે. તેનાં દોલનોનો આવર્તકાળ કેટલો થશે ?View Solution
- 5$2k$ અને $9k$ બળ અચળાંક ધરાવતી બે દળ રહિત સ્પ્રિંગોના મુક્ત છડે $50\, g$ અને $100 \,g$ દળો લટકાવેલા છે. આ દળો શિરોલંબ દિશામાં એવી રીતે દોલનો કરે છે કે જેથી તેમના મહત્તમ વેગો સમાન થાય. તો તેઓના અનુક્રમે કંપ વિસ્તારોનો ગુણોત્તર.....થશે.View Solution
- 6આકૃતિ $-1$ માં દર્શાવ્યા પ્રમાણે $k$ બળ અચળાંક ધરાવતી સ્પ્રિંગના છેડે $M$ દળનો પદાર્થ જોડેલો છે.અને આકૃતિ $-2$ સ્પ્રિંગમાંશ્રેણીમાં જોડેલ છે. જો તેમના આવર્તકાળનો ગુણોત્તર $\frac{ T _{ b }}{ T _{ a }}=\sqrt{ x }$ હોય તો $x$નું મૂલ્ય નજીકના પૂર્ણાંકમાં કેટલું હશે?View Solution
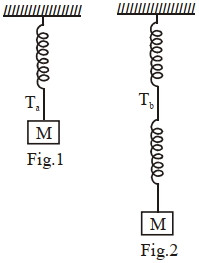
- 7$L$ લંબાઈ અને $A$ આડછેડનું ક્ષેત્રફળ ધરાવતા તારના છેડે એક $m$ દળનો પદાર્થ જોડેલ છે. તારના દ્રવ્યનો યંગ મોડ્યુલસ $Y$ છે. જો આ પદાર્થને થોડોક ખેંચીને મુક્ત કરવામાં આવે તો તે શિરોલંબ દિશામાં આવર્ત ગતિ કરે તો આ ગતિની આવૃતિ કેટલી હશે?View Solution
- 8સમતોલન સ્થાન પાસેથી સરળ આવર્ત ગતિ શરૂ કરતાં પદાર્થનો કંપવિસ્તાર $A$ અને આવર્તકાળ $T$ છે.સમતોલન સ્થિતિથી $ X = \frac{A}{2} $ અંતરે વેગ કેટલો થાય?View Solution
- 9$LCR$ પરિપથ એ અવમંદિત દોલકને સમતુલ્ય છે.નીચે દર્શાવ્યા મુજબ સંઘારક ને $Q_0$ જેટલા વિદ્યુતભારથી વીજભારિત કરેલ છે.અને ત્યારબાદ તેને $L$ અને $R$ સાથે જોડવામાં આવે છે. જો વિદ્યાર્થી, બે જુદાં-જુદાં $L_1$ અને $L_2$ $(L_1 > L_2)$ મૂલ્યોના ઇન્ડકટર માટે સંઘારક પરના મહત્તમ વિદ્યુતભારના વર્ગ $( Q^2_{max})$ વિરુદ્વ સમય માટેના ગ્રાફ દોરે,તો નીચે આપેલમાંથી કયો ગ્રાફ તેને સાચી રીતે રજૂ કરશે? (આકૃતિ રેખાકૃતિ છે અને તે એક જ સ્કેલ પર દોરેલ નથી. )View Solution
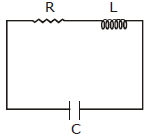
- 10એક $d$ ઘનતાવાળા લાકડાનો ઘન તેની ઉપરની અને નીચેની સપાટી સમક્ષિતિજ રહે તે રીતે $\rho$ ઘનતાવાળા પ્રવાહીમાં તરે છે. ઘનની લંબાઈ $l$ છે. જો ઘનને અધો દિશામાં થોડુક બળ આપીને છોડી દેવામાં આવે, તો તે $T$ આવર્તકાળથી સરળ આવર્તગતિ કરે છે. તો $T$ નું મૂલ્ય $=$View Solution
