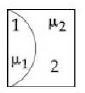
$R$ ત્રિજ્યા ધરાવતા અલગ અલગ પદાર્થમાથી બનેલા સમતલ અંતર્ગોળ અને સમતલ બહિર્ગોળ લેન્સને આકૃતિમાં દર્શાવ્યા પ્રમાણે મૂકેલા છે.પહેલા લેન્સનો વક્રીભવનાંક $\mu_1$ અને બીજા લેન્સનો વક્રીભવનાંક $\mu_2$ હોયતો તંત્રની સંયુક્ત કેન્દ્રલંબાઇ કેટલી થશે?

JEE MAIN 2019, Diffcult
c
For \(1^{\text {st }}\) lens \(\frac{1}{{{f_1}}} = \left( {\frac{{{\mu _1} - 1}}{1}} \right)\) \(\left( {\frac{1}{\infty } - \frac{1}{{ - R}}} \right) = \frac{{{\mu _1} - 1}}{R}\)
For \(1^{\text {st }}\) lens \(\frac{1}{{{f_1}}} = \left( {\frac{{{\mu _1} - 1}}{1}} \right)\) \(\left( {\frac{1}{\infty } - \frac{1}{{ - R}}} \right) = \frac{{{\mu _1} - 1}}{R}\)
For \(2^{n d}\) lens \(\frac{1}{{{f_2}}} = \left( {\frac{{{\mu _2} - 1}}{1}} \right)\) \(\left( {\frac{1}{{ - R}} - 0} \right) = - \frac{{{\mu _2} - 1}}{R}\)
\(\frac{1}{f_{e q}}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)
\(\frac{1}{{{f_{eq}}}} = \frac{{{\mu _1} - 1}}{R} + \frac{{ - \left( {{\mu _2} - 1} \right)}}{R}\) \( \Rightarrow {f_{eq}} = \frac{R}{{{\mu _1} - {\mu _2}}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પાતળા બહિર્ગોળ લેન્સ માટે વક્રતાત્રિજ્યા અનુકુમે $15 \mathrm{~cm}$ અને $30 \mathrm{~cm}$ છે. લેન્સની કેન્દ્ર લંબાઈ $20 \mathrm{~cm}$ હોય તો દ્રવ્યનો વક્રીભવનાંક. . . . . . . હશે.View Solution
- 2ચોરસ ખાના ધરાવતી એક તારની જાળીને (મેશ) $10\,cm$ કેન્દ્ર લંબાઈ ધરાવતા બહિગોળ લેન્સથી $8\,cm$ મુકીને જોતા મોટવણી કેટલી મળે?View Solution
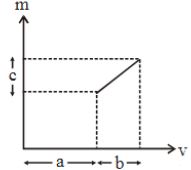
- 3પાતળા લેન્સ માટે મોટવણી $m$ વિરુદ્ધ પ્રતિબિંબ અંતર $v$ નો આલેખ આપેલ છે.તો લેન્સની કેન્દ્રલંબાઈ કેટલી હશે?View Solution
- 4આકતિમાં દર્શાવ્યા મુજબ $1.5$ વક્રીભવનાંકનો કાચનો પ્રિઝમ પાણી $(_a\mu_w = 4/3)$ માં ડૂબાડેલો છે. પ્રકાશનું પુંજ $AB$ બાજુને લંબ આપાત થઈ સંપૂર્ણ પણે $BC$ પરથી પરાવર્તન પામે છે.View Solution

- 5View Solutionનીચેનામાંથી ક્યુ વિધાન સાચુ છે ?
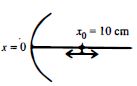
- 6$x_0 = 10\, cm$ પર રહેલ એક કણ $X-$ અક્ષ પર $2\, cm$ ના કંપવિસ્તાર અને $\omega $ આવૃતિથી દોલનો કરે છે.આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $5\,cm$ કેન્દ્રલંબાઈ ધરાવતો અંતર્ગોળ અરીસો ઉગમબિંદુ પાસે છે. તો નીચે પૈકી કયા વિષનો સાચા પડશે.View Solution
$(A)$ પ્રતિબિંબ આવર્તનીય ગતિ કરે
$(B)$ પ્રતિબિંબ આવર્તનીય ગતિ કરશે નહીં
$(C)$ પ્રતિબિંબના મહત્તમ અને ન્યૂનતમ અંતર $x =10\,cm$ સાપેક્ષે અસંમિત હશે
$(D)$ પ્રતિબિંબના મહત્તમ અને ન્યૂનતમ અંતરનો તફાવત $\frac{{100}}{{21}}$ જેટલો હશે
- 7ટેલિસ્કોપ બનાવવા માટે $\pm 15\; cm$ અને $\pm 150 \;cm$ કેન્દ્રલંબાઇ ધરાવતા અલગ અલગ ચાર લેન્સ આપેલા છે. મોટી મોટવણી મેળવવા માટે નેત્રકાંચની કેન્દ્રલંબાઈ ($cm$ માં) કેટલી હોવી જોઇએ?View Solution
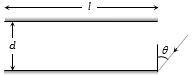
- 8પ્રિઝમનો લઘુત્તમ વિચલનકોણ $40^o $ અને પ્રિઝમકોણ $60^o $ હોય,તો આપાતકોણ કેટલા ......$^o$ હશે?View Solution
- 9View Solutionઆપેલ આકૃતિમાં રહેલ કિરણ બહાર નીકળે ત્યારે તેનું કેટલી વખત પરાવર્તન થશે?
- 10$2000 \,\,m$ ઉંચાઈએ ઉડી રહેલા વિમાન દ્વારા જમીન પરનો ફોટોગ્રાફ $ 50\,\, cm$ કેન્દ્રલંબાઈના લેન્સ ધરાવતા કેમેરા વડે લેવામાં આવે છે. કેમેરામાં ફીલ્મનું કદ $18\,\, cm × 18\,\, cm$ છે. કોઈ એક સમયે આ કેમેરા વડે ફોટોગ્રાફ પાડી શકાતા સપાટીનું ક્ષેત્રફળ કેટલું હશે?View Solution
