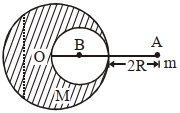
$R$ ત્રિજ્યા ધરાવતો એક ઘન ગોળો તેના કેન્દ્રથી $3R$ અંતરે રહેલા કણને $F_1$ જેટલા બળ દ્વારા ગુરુત્વાકર્ષણ બળ થી આકર્ષે છે. હવે, ગોળામાં $\left(\frac{R}{2}\right)$ જેટલી ગોલીય બખોલ (છિદ્ર) કરવામાં આવે છે (આકૃત્તિમાં દર્શાવ્યા મુજબ) અને બળ $F_2$ થાય છે. $F _{1}: F _{2}$ નું મૂલ્ય ........... છે.
JEE MAIN 2021, Diffcult
Download our app for free and get started
c
Let initial mass of sphere is \(m ^{\prime} .\) Hence mass of removed portion will be \(m ^{\prime} / 8\)
Let initial mass of sphere is \(m ^{\prime} .\) Hence mass of removed portion will be \(m ^{\prime} / 8\)
\(F _{1}= m . E .=\frac{ m \cdot Gm ^{\prime}}{9 R ^{2}}\)
\(F_{2}=m\left[\frac{G \cdot m^{\prime}}{(3 R)^{2}}-\frac{G \cdot m^{\prime} / 8}{(5 R / 2)^{2}}\right]\)
\(=\frac{G m^{\prime}}{9 R^{2}}-\frac{G m^{\prime} \times 4}{8 \times 25}\)
\(=\left(\frac{1}{9}-\frac{1}{50}\right) \frac{G m^{\prime}}{R^{2}}\)
\(F_{2}=\frac{41}{50 \times 9} \cdot \frac{G m^{\prime}}{R^{2}}\)
\(\frac{F_{1}}{F_{2}}=\frac{1}{9} \times \frac{50 \times 9}{41}=\frac{50}{41}\)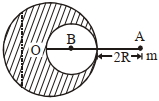
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$M$ દળ ધરાવતો કણ સમાન દળ અને $a$ ત્રિજયા ઘરાવતી ગોળીય કવચના કેન્દ્ર પર છે. તેના કેન્દ્રથી $\frac{a}{2}$ અંતરે ગુરુત્વસ્થિતિમાન મૂલ્ય કેટલું થાય?View Solution
- 2પૃથ્વી અને સૂર્ય વચ્ચેનું મહત્તમ અને ન્યૂનતમ અંતર $r_1 $ અને $r_2$ છે, જ્યારે તે સૂર્યથી દોરેલી ભ્રમણકક્ષાના મુખ્ય અક્ષને લંબ પર હોય ત્યારે તેનું સૂર્યથી અંતર કેટલું હશે?View Solution
- 3View Solutionકેપ્લરનો બીજો નિયમ કયા નિયમના સંરક્ષણથી મળે છે.
- 4ચંદ્ર અને પૃથ્વીના કેન્દ્ર વચ્ચેનું અંતર $D$ છે.જો પૃથ્વીનું દળ ચંદ્ર કરતાં $81$ ગણું હોય,તો પૃથ્વીના કેન્દ્રથી કેટલા અંતરે ગુરુત્વાકર્ષણ બળ શૂન્ય થાયView Solution
- 5પૃથ્વીની ત્રિજ્યા અને દળમાં $0.5\%$ નો વધારો થાય તો નીચેનામાથી પૃથ્વીની સપાટી માટે શું સાચું છેView Solution
- 6વ્યક્તિને વધુ માત્રામાં પદાર્થનો જથ્થો $kg-wt$ માં ક્યાં મળે?View Solution
- 7એક પદાર્થને પૃથ્વીની ત્રિજ્યા $(R)$ જેટલી ઉંયાઈએથી મુક્ત કરવામાં આવે છે. જ્યારે તે પૃથ્વીની સપાટી પર અથડાય ત્યારે તેનો વેગ ........... હશે. ($g$ =પૃથ્વીનો ગુરુત્વ પ્રવેગ આપેલ છે.)View Solution
- 8દળ વિતરણ ને લીધે $X-$દિશામાં ગુરુત્વાકર્ષી ક્ષેત્ર $E = K/{x^3}$ ($K$ અચળાંક છે). અનંત અંતરે શૂન્ય હોય તો $X$ અંતરે ગુરુત્વસ્થિતિમાનનું મુલ્ય કેટલું થાય?View Solution
- 9કેપ્લરના ત્રીજા નિયમ મુજબ, સૂર્યનું પરિભ્રમણ કરતા ગ્રહનો આવર્તકાળ $(T)$ તે ગ્રહ અને સૂર્ય વચ્ચેના સરેરાશ અંતર $r$ ની ત્રણ ઘાતના સમપ્રમાણમાં છે.View Solution
$\therefore {T^2} = k{r^3}$,
જયાં $K$ અચળાંક છે.
જો સૂર્યનું અને ગ્રહનું દળ અનુક્રમે $M$ અને $m$ હોય, તો ન્યુટનના ગુરુત્વાકર્ષણના નિયમ પરથી તેમની વચ્ચે લાગતું ગુરુત્વાકર્ષણ બળ $F = \frac{{GMm}}{{{r^2}}}$, જયાં $G =$ ગુરુત્વાકર્ષણનો અચળાંક છે. $G$ અને $K$ વચ્ચેનો સંબંઘ શેના વડે દર્શાવી શકાય?
- 10એક ઉપગ્રહની કક્ષીય ત્રિજ્યા સંચાર ઉપગ્રહની કક્ષીય ત્રિજ્યા કરતાં $4$ ગણી છે તો તે ઉપગ્રહનો પરિભ્રમણ સમય ...... $day$ થાય.View Solution