$\mathrm{R}$ ત્રિજ્યા ધરાવતો લાંબો સોલેનોઇડ સમય સાથે ફરતા પ્રવાહ $\mathrm{I}(\mathrm{t})=\mathrm{I}_{0} \mathrm{t}(1-\mathrm{t})$ નું વહન કરે છે. $2 \mathrm{R}$ ત્રિજ્યાની રિંગને તેને સમઅક્ષીય રીતે રહે તેમ તેના મધ્યમાં મૂકવામાં આવે છે. $0 \leq t \leq 1$,સમય દરમિયાન રિંગમાં પ્રેરિત પ્રવાહ $\left(\mathrm{I}_{\mathrm{R}}\right)$ અને પ્રેરિત $\mathrm{EMF}\left(\mathrm{V}_{\mathrm{R}}\right)$ કઈ રીતે બદલાય?
JEE MAIN 2020, Diffcult
a
Magnetic flux ( \(\phi\) ) through ring is \(\phi=\pi(R)^{2} . B\)
Magnetic flux ( \(\phi\) ) through ring is \(\phi=\pi(R)^{2} . B\)
\(\phi=\left(\pi \mathrm{R}^{2}\right)\left(\mu_{0} \mathrm{n} \mathrm{I}\right)=\left(\pi \mathrm{R}^{2} \mu_{0} \mathrm{n} \mathrm{I}_{0}\right)\left(\mathrm{t}-\mathrm{t}^{2}\right)\)
Induced e.m.f. of \(\mathrm{V}_{\mathrm{R}}=\frac{-\mathrm{d} \phi}{\mathrm{dt}}\)
\(=\left(\pi \mathrm{R}^{2} \mu_{0} \mathrm{nI}_{0}\right)(2 \mathrm{t}-1)\)
and induced current \(\mathrm{I}_{\mathrm{R}}=\frac{\pi \mathrm{R}^{2} \mu_{0} \mathrm{nI}_{0}(2 \mathrm{t}-1)}{\mathrm{R}_{\mathrm{R}}}\)
\(\left(\mathrm{R}_{\mathrm{R}} \rightarrow \text { Resistance of Ring }\right)\)
Clearly \(\mathrm{V}_{\mathrm{R}}\) and \(\mathrm{I}_{\mathrm{R}}\) are zero at \(\mathrm{t}=\frac{1}{2}=0.5 \mathrm{sec}\)
and their sign also changes at \(t=0.5\) sec.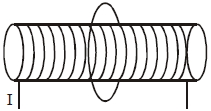
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10 \mathrm{~cm}$ બાજુ અને $0.7 \Omega$ અવરોધની એક ચોરસ લૂપને પૂર્વ-પશ્રિમ સમતલમાં શિરોલંબ રાખેલી છે.$0.20$$T$ મૂલ્યના સમાન ચુંબકીય ક્ષેત્રને ઉત્તર-પૂર્વ દિશામાંના સમતલમાં રાખેલ છે. ચુંબકીય ક્ષેત્ર $1 S$ માં સ્થિર દરે ધટીને શૂન્ય થાય છે. તો પ્રેરિત emf નું મૂલ્ય $\sqrt{x} \times 10^{-3} V$ છે. તો $x$ નું મૂલ્ય________છે.View Solution
- 2$5000$ આંટા અને $ 0.25\,{m^2} $ ક્ષેત્રફળ ધરાવતી કોઇલ જનરેટરમાં વાપરવામાં આવે છે,કોઇલ $0.2$ $ W/{m^2} $ ચુંબકીયક્ષેત્રમાં $100$ પરિભ્રમણ/sec ની કોણીય ઝડપથી ભ્રમણ કરતાં કેટલા ......$kV$ મહત્તમ $emf$ ઉત્પન્ન થાય?View Solution
- 3$20 \;m$ લંબાઇનો એક સુરુખ તાર પૂર્વથી પશ્વિમ દિશામાં રાખેલો છે. તે પૃથ્વીના ચુંબકીય ક્ષેત્ર $0.30 \times 10^{-4} wb / m ^{2}$ ના સમક્ષિતિજ ઘટકને કાટખૂણે, $5.0\; m / s$ ના વેગથી નીચે પડે છે. તારની અંદર ઉત્પન્ન થતા તત્કાલીન $emf$ નું મૂલ્ય કેટલું હશે ?View Solution
- 4કોઇલમાં પ્રવાહ $8\, A$ થી $2 \,A$ , $ 3 \times {10^{ - 2}} $ $second$ માં કરતાં $2\, V$ $emf$ ઉત્પન્ન થાય છે.તો કોઇલનું આત્મપ્રેરકત્વ કેટલું થાય? (in $millihenry$)View Solution
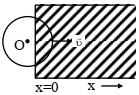
- 5${x}\,>\,0$ વિસ્તારમાં $1 \,{T}$ જેટલું અચળ ચુંબકીયક્ષેત્ર લગાવવામાં આવે છે. $1 \,{m}$ ત્રિજ્યા ધરાવતી વર્તુળાકાર રિંગ $1 \,{m} / {s}$ aના વેગથી $x-$ અક્ષ પર ગતિ કરે છે. $t=0s$ સમયે તેનું કેન્દ્ર ${x}=-1 \,{m}$ પર છે. $t=1\, s$ સમયે તેમાં ઉદ્ભવતો $emf$ (${V}$ માં) કેટલો હશે? (રિંગનો વેગ બદલાતો નથી તેમ ધારો) (In ${V}$)View Solution
- 6એક ગૂંચળાની પ્રેરકતા $2\; H$ અને અવરોધ $4\,\Omega$ છે. $10\,V$ નું $emf$ ગૂંચળામાંથી પસાર કરવામાં આવે છે. ચુંબકીયક્ષેત્રને લીધે વીજપ્રવાહ તેની સંતુલન કિમત સાથે સંકળાય છે, ત્યારની ઊર્જા ........ $\times 10^{-2}\,J$ હશે.View Solution
- 7એક આદર્શ $10\, H$ ઇન્ડકટર અને $5 \,\Omega$ અવરોધને $5\, V$ની બેટરી સાથે શ્રેણીમાં લગાવતા $2 \,s$ પછી પરિપથમાંથી કેટલો પ્રવાહ(એમ્પિયરમાં) પસાર થશે?View Solution
- 8કોઇલમાં ઉદ્ભવતું emf, વિદ્યુતપ્રવાહ અને વિદ્યુતભાર અનુક્રમે $ E,\;I $ અને $ Q $ છે,જો ચુંબકની ઝડપ બમણી કરવામાં આવે,તો નીચેનામાથી શું ખોટું થાય?View Solution
- 9તાંબાની ડિસ્કની ત્રિજ્યા $0.1\,m$ છે તથા તે તેમાં કેન્દ્રથી $10$ $rev / s$ નાં વેગથી ભ્રમણ કરે છે તથા તેનું ભ્રમણ $0.1\,T$ જેટલા સમાન ચુંબકીય ક્ષેત્રને લંબ છે. તો તક્તીમાં પ્રેરીત થતું $emf$......... $volt$View Solution
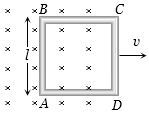
- 10$l$ લંબાઇની બાજુવાળો અને $R$ અવરોધ ધરાવતી વાહક ચોરસ લૂપ તેના સમતલમાં એકસમાન વેગ $v$ થી તેની એક બાજુને લંબ રહે તેમ ગતિ કરે છે. આકૃતિમાં દર્શાવ્યા મુજબ સમય અને સ્થાન સાથે સમાન ચુંબકીયક્ષેત્ર $B$ સમતલની અંદરની દિશામાં છે. ઉત્પન્ન થતું $e.m.f.$ કેટલું હશે?View Solution