$r $ ત્રિજયાના કોઇ વિસ્તારમાં એકસમાન ચુંબકીયક્ષેત્ર છે. આ ચુંબકીયક્ષેત્રમાં સમય સાથે $\frac{{d\vec B}}{{dt}}$ ના દરથી ફેરફાર થાય છે. આકૃતિમાં દર્શાવ્યા અનુસાર $R$ નું $(R>r) $ લૂપ $-1,r $ ત્રિજયાના લૂપને ઘેરાયેલું છે,તથા $ R$ ત્રિજયાનું લૂપ $- 2$ ચુંબકીયક્ષેત્રના વિસ્તારની બહાર છે. તો ઉત્પન્ન થયેલ $emf$ નું મૂલ્ય કેટલું હશે?
NEET 2016, Medium
Download our app for free and get started
b
\(Emf\) generated in loop \(1\),
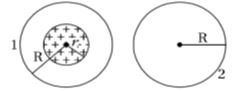
\(Emf\) generated in loop \(1\),
\(\varepsilon_{1}=-\frac{d \phi}{d t}=-\frac{d}{d t}(\vec{B} \cdot \vec{A})=-\frac{d}{d t}(B A)=-A \times \frac{d B}{d t}\)
\(\varepsilon_{1}=-\left(\pi r^{2} \frac{d B}{d t}\right)\)
\(( \because A=\pi r^{2} \text { because } \frac{d B}{d t}\) is restricted upto radius \(r.).\)
\(Emf\) generated in loop \(2\),
\(\varepsilon_{2}=-\frac{d}{d t}(B A)=-\frac{d}{d t}(0 \times A)=0\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ગૂંચળામાં પ્રવાહના ફેરફાર $0.01\,A$ કરતા બીજા ગૂંચળાના ફ્લકસમા ફેરફાર $2 \times {10^{ - 2}}\,Wb$ થાય તો અનોન્ય પ્રેરકત્વ ......$henry$View Solution
- 2એક $12\,V,60\,W$ના લેમ્પને સ્ટેપડાઉન ટ્રાન્સફાર્મરના ગૌણ છેડા $(secondary)$ સાથે જોડેલ છે, જ્યારે તેના પ્રાથમિક છેડા $(primary)$ને $220\,V$ના એસી મેઈન્સ સાથે જોડવામોં આવે છે.જો ટ્રાન્સફોર્મરને આદર્શ ધારવામાં આવે તો, પ્રાથમિક ગૂંચળામાં $.......\,A$ પ્રવાહ વહેશે.View Solution
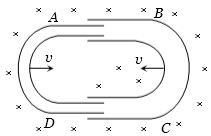
- 3આકૃતિમાં દર્શાવ્યા મુજબ એક $U$ આકારની વાહક ટ્યુબ બીજી વાહક ટ્યુબની અંદર એવી રીતે સરકે છે કે જેથી તેમની વચ્ચે વિદ્યુતીય સંપર્ક રહે છે.આકૃતિમાં દર્શાવ્યા મુજબ ચુંબકીયક્ષેત્ર $B$ સમતલને લંબ રીતે પ્રવતે છે.બંને ટ્યુબ એકબીજા તરફ $v$ વેગથી ગતિ કરતી હોય તો તેમાં કેટલો $emf$ ઉત્પન્ન થશે?View Solution
જ્યાં $l$ દરેક ટ્યુબની પહોળાય છે.
- 4$10 \,\Omega, 20 \,mH$ ના ગૂંચળું કે જેમાંથી અચળ પ્રવાહ પસાર થાય છે. ને કળ દ્વારા $20 \,V$ ની બેટરી સાથે જોડવામાં આવે છે. $100 \,\mu s$ પછી કળને ખોલવામાં આવે છે. ગૂંચળાંમાં પ્રેરિત સરેરાશ $e.m.f.$ ............ $V$ થશે.View Solution
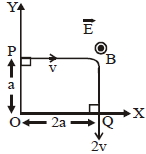
- 5$\mathrm{m}$ દળ અને $q$ વિજભાર ધરાવતો કણ $E\hat{i }$ વિદ્યુતક્ષેત્ર અને $B\hat{k}$ ચુંબકીયક્ષેત્ર ની અંદર બિંદુ $\mathrm{P}$ થી બિંદુ $\mathrm{Q}$ તરફ આકૃતિમાં દર્શાવ્યા પ્રમાણે ગતિ કરે છે. $P$ અને $Q$ બિંદુ આગળ કણનો વેગ અનુક્રમે $v\hat i$ અને $-2 v \hat j$ છે. તો નીચે આપેલા ચાર વિધાન $(\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D})$ માથી ક્યાં સાચા પડે?View Solution
$(A)$ $\mathrm{E}=\frac{3}{4}\left(\frac{\mathrm{mv}^{2}}{\mathrm{qa}}\right)$
$(B)$ $\mathrm{P}$ બિંદુ આગળ વિદ્યુતક્ષેત્રને કારણે થતાં કાર્યનો દર $\frac{3}{4}\left(\frac{\mathrm{mv}^{3}}{\mathrm{a}}\right)$
$(C)$ $\mathrm{Q}$ બિંદુ આગળ બંને ક્ષેત્રને કારણે થતાં કાર્યનો દર શૂન્ય થાય.
$(D)$ $\mathrm{P}$ અને $\mathrm{Q}$ બિંદુ આગળ મળતા કોણીય વેગમાનના મૂલ્યનો તફાવત $2 mav$ થાય.
- 6View Solutionટ્રાન્સફોર્મર શું કાર્ય કરે છે?
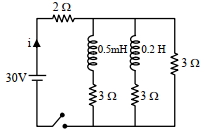
- 7આપેલ પરિપથમાં જ્યારે કળ બંધ કરીને અને સ્થાયી સ્થિતિ પ્રાપ્ત કરે ત્યારે તેમાંથી પસાર થતો પ્રવાહ $i$ ($A$ માં) કેટલો હશે?View Solution
- 8બે સમકેન્દ્રિત વર્તુળાકાર કોઇલ જે $1\,cm$ અને $1000\,cm$ ત્રિજ્યા અને અનુક્રમે $10$ અને $200$ આંટાની સંખ્યા ધરાવતા હોય, તેમને તેના કેન્દ્રો સમાન અક્ષ પર સંપાત થાય તેમ મૂકેલા છે આ તંત્રનું આત્મ પ્રેરકત્વ ......... $\times 10^{-8}\,H$ હશે. ($\pi^2=10$ લો)View Solution
- 9$10\,cm$ ત્રિજ્યા ધરાવતી કોઈલ નું સમતલન $3.0 \times 10^{-5}\, T$ ના ચુબકીયક્ષેત્ર ને લંબ મૂકેલી છે. કોઈલના વ્યાસને અનુલક્ષીને અને ચુબકીયક્ષેત્રને લંબ અક્ષને અચળ કોણીય ઝડપથી ફેરવવામાં આવે છે. $0.2\,Sec$ માં અડધુ પરિભ્રમણ કરે છે. કોઇલમાં ઉદભવતું મહતમ $emf.......\mu V$View Solution
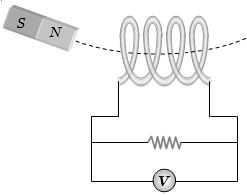
- 10ચુંબક આકૃતિ મુજબ દોલન કરે છે,તો $1$ દોલન દરમિયાન કોઇલમાં ઉદ્ભવતા $emf$ વિરુધ્ધ સમયનો આલેખ કેવો થાય?View Solution
