$R$ ત્રિજ્યાનો અવાહક ધન ગોળો સમાન રીતે વિદ્યુતભારીત થયેલો છે. તેના કેન્દ્રથી $r$ અંતરે આવેલ ગોળાને લીધે વિદ્યુતક્ષેત્રનું મૂલ્ય ........ છે.
$(1)\, r$ ના વધારા સાથે વધે છે $r < R \,$
$(2)\, r$ ના વધારા સાથે ઘટશે $0 < r <$ $\infty$
$(3)\, r$ ના વધારા સાથે ઘટશે $R < r < \infty \,$
$(4)\, r = R$ આગળ તે સતત છે.
Medium
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો બંધ પૃષ્ઠમાં દાખલ થતું અને બહાર આવતું ફલક્સ અનુક્રમે $\phi_1$ અને $\phi_2$ છે. પૃષ્ઠની અંદરની બાજુએ વિદ્યુતભાર ........ હશે.View Solution
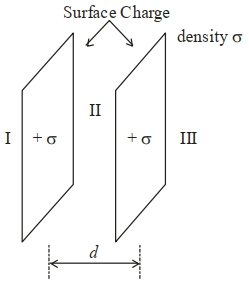
- 2આકૃતિમાં બતાવેલ બે અનંત પાતળા સમતલની પૃષ્ઠ વિદ્યુતભાર ઘનતા $\sigma$ છે. તો ત્રણ જુદા જુદા પ્રદેશ $E_{ I }, E_{ II }$ અને $E_{III}$ માં વિદ્યુતક્ષેત્ર કેટલું મળે?View Solution
- 3જ્યારે પોલીથીનના એક ટુકડાને ઊન સાથે ઘસવામાં આવે તો પોલીથીન પર $-2 -\times 10^{-7}\ C$ જેટલો વિદ્યુતભાર ઉત્પન્ન થાય છે. દળનો કેટલો જથ્થો પોલીથીન તરફ વહન પામતો હશે?View Solution
- 4જેની દ્વિ ધ્રુવીય ચાકમાત્રા $P$ અને જડત્વની ચાકમાત્રા $I$ હોય તેવા વિદ્યુત ક્ષેત્રની સમાન તીવ્રતા વાળા ક્ષેત્રમાં વિદ્યુત ડાઈપોલને ગોઠવેલી છે. ડાઈપોલને ફેરવવામાં આવે તો તેના દોલનની કોણીય આવૃત્તિ ........ છે.View Solution
- 5સાચું વિધાન પસંદ કરો.View Solution
$(1)$ બળ રેખા પરના કોઈ પણ બિંદુ આગળ દોરેલો સ્પર્શક એ આપેલ બિંદુ આગળ ધન વિદ્યુતભાર પર લાગતા બળની દિશા આપે છે.
$(2)$ બળ રેખા પરના કોઈ પણ બિંદુ આગળ દોરેલ લંબ એ આપેલ બિંદુ આગળ ધન વિદ્યુતભાર પર લાગતા બળની દિશા આપે છે.
$(3)$ બળની વિદ્યુત રેખાઓ ઋણ વિદ્યુતભાર થી શરૂ કરીને ધન વિદ્યુતભાર પર પૂર્ણ થાય છે.
$(4)$ બળની વિદ્યુત રેખાઓ ધન વિદ્યુતભાર થી શરૂ કરીને ઋણ વિદ્યુતભાર પર પૂર્ણ થાય છે.
- 6View Solutionઇલેક્ટ્રીક ડાઈપોલને અસમાન વિધુતક્ષેત્રમાં મુક્તા તે .............. અનુભવે છે
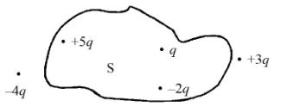
- 7પાંચ વિદ્યુતભારો $+q,+5 q,-2 q,+3 q$ અને $-4 q$ ને આક્રૂત્તિમાં દર્શાવ્યા અનુસાર ગોઠવવામાં આવ્યા છે.View Solution
સપાટી $s$ માંથી પસાર થતું આ વિદ્યુતભારોની ગોઠવણીને કારણે સંકળાયેલ ફ્લક્સ...........છે.
- 8એક ગોળા પર એકસમાન વિજભાર પથરાયેલ છે તેની વિજભાર ઘનતા નીચે મુજબ આપવામાં આવે છે.View Solution
$\rho (r)\, = \,{\rho _0}\left( {1 - \frac{r}{R}} \right)$, $r < R$ માટે
$\rho (r)\,=\,0$, $r\, \ge \,R$ માટે
જ્યાં $r$ એ વિજભાર વિતરણના કેન્દ્રથી અંતર અને $\rho _0$ અચળાંક છે. $(r < R)$ ના અંદરના બિંદુ પાસે વિદ્યુતક્ષેત્ર કેટલું મળે?
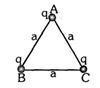
- 9આકૃતિમાં $A$ આગળના વિદ્યુતભાર પરનું બળ $BC$ ને લંબ દિશામાં ...... હશે.View Solution
- 10ચાર સમાન વિદ્યુતભારોને ચોરસના ચારેય ખૂણા પર મૂકેલા છે. કોઈ પણ એક વિદ્યુતભારને લીધે ચોરસના કેન્દ્ર આગળ વિદ્યુતભારની તીવ્રતા $E$ હોય તો ચોરસના કેન્દ્ર આગળ પરિણામી વિદ્યુતક્ષેત્રની તીવ્રતા ....... હશે.View Solution