જેની દ્વિ ધ્રુવીય ચાકમાત્રા $P$ અને જડત્વની ચાકમાત્રા $I$ હોય તેવા વિદ્યુત ક્ષેત્રની સમાન તીવ્રતા વાળા ક્ષેત્રમાં વિદ્યુત ડાઈપોલને ગોઠવેલી છે. ડાઈપોલને ફેરવવામાં આવે તો તેના દોલનની કોણીય આવૃત્તિ ........ છે.
Diffcult
a
(a) When dipole is given a small angular displacement \(\theta \) about it's equilibrium position, the restoring torque will be
\(\tau = - \,pE\sin \theta = - \,pE\theta \) (as \( \sin\theta = \theta \))
(a) When dipole is given a small angular displacement \(\theta \) about it's equilibrium position, the restoring torque will be
\(\tau = - \,pE\sin \theta = - \,pE\theta \) (as \( \sin\theta = \theta \))
or \(I\frac{{{d^2}\theta }}{{d{t^2}}} = - pE\theta \) (as \(\tau = I\alpha = I\frac{{{d^2}\theta }}{{d{t^2}}}\))
or \(\frac{{{d^2}\theta }}{{d{t^2}}} = - {\omega ^2}\theta \) with \({\omega ^2} = \frac{{pE}}{I}\) \(==>\) \(\omega = \sqrt {\frac{{pE}}{I}} \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$e$ વિદ્યુતભાર ધરાવતો અને $m$ દળ ધરાવતો ઇલેક્ટ્રોનને સમાન વિદ્યુતક્ષેત્ર $E$ માં મૂકવામાં આવે તો તેનો પ્રવેગ કેટલો થશે?View Solution
- 2$6\,m$ ત્રિજ્યા ધરાવતા ગોળાની કદ વિદ્યુતભાર ઘનતા $2\,\mu\,C / cm ^3$ છે. ગોળાની સપાટીમાંથી બહાર આવતી પ્રતિ એકમ પૃષ્ઠ ક્ષેત્રફળ દીઠ બળ રેખાઓની સંખ્યા $..........\times 10^{10} NC ^{-1}$ હશે.View Solution
[Given : Permittivity of vacuum $\left.\epsilon_{0}=8.85 \times 10^{-12} C ^{2} N ^{-1}- m ^{-2}\right]$
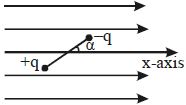
- 3આકૃતિમાં અનિયમિત વિધુતક્ષેત્ર $x-$ અક્ષની દિશામાં છે વિધુતક્ષેત્ર ધન $x-$ અક્ષ પર નિયમિત દરથી વધે છે વિધુતડાઈપોલને વિધુતક્ષેત્રમાં મૂકવામાં આવે છે તો નીચનામાંથી ક્યુ વિધાન સાચું થાય ?View Solution
- 4$ + 3\ \mu C$ અને $ + 8\ \mu C$ વિદ્યુતભાર વચ્ચે લાગતું બળ $40\ N$ છે,બંનેમાં $ - 5\ \mu C$ વિદ્યુતભાર ઉમેરતાં નવું બળ કેટલા ........$N$ થાય?View Solution
- 5$e$ વિદ્યુતભાર ધરાવતો અને $m$ દળ ધરાવતો ઇલેક્ટ્રોનને સમાન વિદ્યુતક્ષેત્ર $E$ માં મૂકવામાં આવે તો તેનો પ્રવેગ કેટલો થશે?View Solution
- 6સમાન વિરૂદ્ધ નિશાની ધરાવતી પૃષ્ઠ વિદ્યુતભાર ઘનતા ($\sigma$ $= 26.4 \times 10^{-12} \ C/m^2$) વાળી બે સમાંતર વિશાળ પાતળી ધાતુની તકતી છે. આ તકતી વચ્ચેનું વિદ્યુતક્ષેત્ર ........$N/C$ છે.View Solution
- 7બે સમાન ગોળાઓ $A$ અને $B$ને જ્યારે હવામાં ચોક્કસ અંતરે રાખવામાં આવે છે ત્યારે તે $F$ જેટલાં બળથી એકબીજાને અપાકર્ષે છે. ત્રીજો સમાન અવિદ્યુતભારીત ગોળો $C$ પ્રથમ ગોળા $A$ના અને ત્યારબાદ ગોળા $B$ના સંપર્કમાં લાવવામાં આવે છે. છેલ્લે તેને ગોળાઓ $A$ અને $B$ ના મધ્યબિંદુ પર મૂકવામાં આવે છે. ગોળા $C$ પર લાગતું બળ $...........$ હશે.View Solution
- 8$R$ ત્રિજ્યાનો અવાહક ધન ગોળો સમાન રીતે વિદ્યુતભારીત થયેલો છે. તેના કેન્દ્રથી $r$ અંતરે આવેલ ગોળાને લીધે વિદ્યુતક્ષેત્રનું મૂલ્ય ........ છે.View Solution
$(1)\, r$ ના વધારા સાથે વધે છે $r < R \,$
$(2)\, r$ ના વધારા સાથે ઘટશે $0 < r <$ $\infty$
$(3)\, r$ ના વધારા સાથે ઘટશે $R < r < \infty \,$
$(4)\, r = R$ આગળ તે સતત છે.
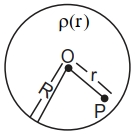
- 9$\rho(r)=\left\{\begin{array}{ll}\rho_{0}\left(\frac{3}{4}-\frac{r}{R}\right) & \text { for } r \leq R \\ \text { Zero } & \text { for } r>R\end{array}\right.$View Solution
અનુસાર બદલાતી ગોલીય સંમિત વિદ્યુતભાર વહેંચણી વિચારો,જ્યાં $r ( r < R )$ એ કેન્દ્રથી અંતર છે (આકૃતિ જુઓ) $P$ બિંદુ આગળ વિદ્યુતક્ષેત્ર $......$ હશે.
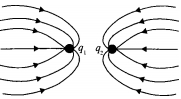
- 10આકૃતિમાં $q_1$ અને $q_2$ બે વિદ્યુતભારને કારણે વિદ્યુતક્ષેત્રરેખા દર્શાવે છે. બે વિદ્યુતભારની સંજ્ઞા કેવી હશે?View Solution