રાસાયણિક સંતુલન માટે, $CaC{{O}_{3}}_{(s)})$ $\rightleftharpoons$ $CaO_{(s)}+C{{O}_{2}}_{(g)},\ \Delta H_{r}^{{}^\circ }$ એ નીચેના પ્લોટમાંથી કયા પ્લોટમાંથી નક્કી કરી શકાય છે.
AIIMS 2005, Diffcult
Download our app for free and get started
a
For the reaction,
For the reaction,
$CaCO_{3(g)} \rightleftharpoons CaO_{(s)} + CO_{2(g)}$
$K_p = P_{CO_2}$ and $K_C = [CO_2]$
$(\because [CaCO_3] = 1$ and $[CaO] = 1$ for solids$)$
According to Arrhenius equation we have
$K = A{e^{ - \Delta H{^\circ _r}/RT}}$
Taking logarithm, we have
$\log {K_p} = \log\, A - \frac{{\Delta H_r^o}}{{RT(2.303)}}$
This is an equation of straight line. When $log \,K_p$ is plotted against $1 / T$. we get a straight line.
The intercept of this line = $ log \,A$, slope $= -\Delta H^°_r / 2.303 \,R$
Knowing the value of slope from the plot and universal gas constant $R$, $∆H^°_r$ can be calculated.
(Equation of straight line : $Y = mx + C$. Here,
$\log {K_p} = - \frac{{\Delta H_r^o}}{{2.303R}}\left( {\frac{1}{T}} \right) + \log A$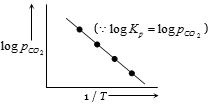
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પ્રકિયા ${H_{2(g)}}\, + \,{I_{2(g)}}\, \rightleftharpoons 2H{I_{(g)}}$ માટે $440\,^oC$ તાપમાને $K_c$ નુ મૂલ્ય $50$ છે. જો પ્રક્રિયાની શરૂઆત $1\,L$ ની ફ્લાસ્કમાં $1$ મોલ $H_ 2$, $2$ મોલ $I_2$ અને $3$ મોલ $HI$ લઇને કરવામાં આવી હોય, તો $HI$ ની સંતુલન સાંદ્રતા .......... $M$ થશે.View Solution
- 2નીચેની પ્રક્રિયા માટે વાયુમય તબક્કામાં .........${K_p}/{K_c}$.View Solution
$CO\left( g \right) + \frac{1}{2}{O_2}\left( g \right) \to C{O_2}\left( g \right)$
- 3View Solutionરાસાયણિક સંતુલન સ્વભાવમાં ગતિશીલ છે કારણ કે
- 4પ્રક્રિયા $CuSO_4.5H_2O_{(s)} $ $\rightleftharpoons$ $ CuSO_4.3H_2O_{(s)} + 2H_2O_{(g)}$ માટે નીચેનામાંથી કયું એક સાચું નિરૂપણ દર્શાવે છે ?View Solution
- 5પ્રકિયા $3A + {\text{ B}}\,\, \rightleftharpoons \,\,2C\, + \,D$ માટે જો $A,\,B$ અને $C$ ની સંતુલન સાંદ્રતાઓ અનુક્રમે $0.03,\, 0.01\,M$ અને $0.008$ હોય, તો $A$ ની શરૂઆતની સાંદ્રતા શું થશે ?View Solution
- 6નીચે આપેલી પ્રતિવર્તી રાસાયણીક પ્રક્રિયા ધ્યાનમાં લો.View Solution
${A_2}(g)\, + \,{B_2}(g)\,\overset {{K_1}} \leftrightarrows \,2AB(g)\,\,\,......(1)$
$6AB\,(g)\,\,\overset {{K_2}} \leftrightarrows \,\,3{A_2}(g)\, + \,3{B_2}(g)......(2)$
તો $K_1$ અને $K_2$ વચ્ચેનો સંબંધ શું થાય?
- 7$1990\, K$ અને $1\, atm$ દબાણ પર, પ્રક્રિયા મિશ્રણમાં $Cl _{2}$ અણુઓ અને $Cl$ પરમાણુઓ સમાન સંખ્યામાં છે. $Cl _{2( g )}=2 Cl _{( g )}$ પ્રક્રિયા માટે ઉપરની પરિસ્થિતિઓ હેઠળ $K_p$ નું મૂલ્ય $x \times 10^{-1}$ છે. તો $x$ નું મૂલ્ય .............. છે. (નજીકના પૂર્ણાકમાં રાઉન્ડ ઑફ)View Solution
- 8પ્રક્રિયા $A + 2B$ $ \rightleftharpoons $ $2C + D$ માં $B$ ની શરૂઆતની સાંદ્રતા $[A]$ કરતા $1.5$ ગણી છે પરંતુ સંતુલને $A$ અને $B$ ની સાંદ્રતાઓ સમાન બને છે. તો પ્રક્રિયા માટે સંતુલન અચળાંક ગણોView Solution
- 9સંતુલન પર, સાંદ્રતાView Solution
$N_{2}=3.0 \times 10^{-3} M$
$O_{2}=4.2 \times 10^{-3} M$
અને $N O=2.8 \times 10^{-3} M$
આપેલ પ્રક્રિયા માટે બંધ કરેલા વાસણમાં $800 \,K$ અને $1$ $atm$ દબાણે $K_{p}$ ......... $atm$ હશે ?
$N_{2}(g)+O_{2}(g) \rightleftharpoons 2 N O(g)$
- 10$400\, K$ તાપમાને $20\, litre$ નુ પાત્ર $0.4$ વાતા. દબાણે $CO_{2(g)}$ અને પૂરતા પ્રમાણમાં $SrO$ ધરાવે છે. (ઘન $SrO$ નું કદ અવગણો) હવે પાત્રમાં ફિટ કરેલા સરકી શકે તેવા પિસ્ટનને ખસેડી પાત્રનું કદ ઘટાડવામાં આવે છે. જ્યારે $CO_{2(g)}$ નુ દબાણ તેનુ મહત્તમ મૂલ્ય પ્રાપ્ત કરે ત્યારે પાત્રનું મહતમ કદ કેટલા ......લિટર થશે ?View Solution
(અહીં : $SrCO_{3(s)} \rightleftharpoons SrO_{(s)}+ CO_{2(g)} \,, K_p=1.6\,atm$)