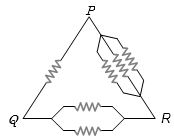
સમાન અવરોધ ધરાવતી આકૃતિમાં મહત્તમ અવરોધ કોના વચ્ચે હશે?

IIT 2004, Diffcult
a
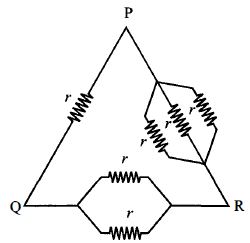
(a) Resistance between \(P\) and \(Q\) \({R_{PQ}} = R||\left( {\frac{R}{3} + \frac{R}{2}} \right)\)\( = \frac{{R \times \frac{5}{6}R}}{{R + \frac{5}{6}R}}\)\( = \frac{5}{{11}}R\)Resistance between \(Q\) and \(R\) \({R_{QR}} = \frac{R}{2}||\left( {R + \frac{R}{3}} \right)\)\( = \frac{{\frac{R}{2} \times \frac{{4R}}{3}}}{{\frac{R}{2} + \frac{{4R}}{3}}}\)\( = \frac{4}{{11}}R\)Resistance between \(P\) and \(R\) \({R_{PR}} = \frac{R}{3}||\left( {\frac{R}{2} + R} \right)\)\( = \frac{{\frac{R}{3} \times \frac{{3R}}{2}}}{{\frac{R}{3} + \frac{{3R}}{2}}}\)\( = \frac{3}{{11}}R\) Hence it is clear that \({P_{PQ}}\) is maximum.
(a) Resistance between \(P\) and \(Q\) \({R_{PQ}} = R||\left( {\frac{R}{3} + \frac{R}{2}} \right)\)\( = \frac{{R \times \frac{5}{6}R}}{{R + \frac{5}{6}R}}\)\( = \frac{5}{{11}}R\)Resistance between \(Q\) and \(R\) \({R_{QR}} = \frac{R}{2}||\left( {R + \frac{R}{3}} \right)\)\( = \frac{{\frac{R}{2} \times \frac{{4R}}{3}}}{{\frac{R}{2} + \frac{{4R}}{3}}}\)\( = \frac{4}{{11}}R\)Resistance between \(P\) and \(R\) \({R_{PR}} = \frac{R}{3}||\left( {\frac{R}{2} + R} \right)\)\( = \frac{{\frac{R}{3} \times \frac{{3R}}{2}}}{{\frac{R}{3} + \frac{{3R}}{2}}}\)\( = \frac{3}{{11}}R\) Hence it is clear that \({P_{PQ}}\) is maximum.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
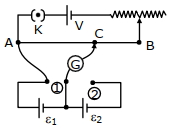
- 1આપેલ પોટેન્ટિયોમીટર પરિપથની ગોઠવણીમાં, તટસ્થ બિંદુ માટે ${AC}$ ની લંબાઈ $250\;cm$ માપવામાં આવે છે. જ્યારે ગેલ્વેનોમીટરનું જોડાણ આકૃતિમાં રહેલ બિંદુ $(1)$ થી બિંદુ $(2)$ પર કરવામાં આવે ત્યારે સંતુલન લંબાઈ $400\, {cm}$ થાય છે. બે કોષોના $e.m.f.$ નો ગુણોત્તર, $\frac{\varepsilon_{1}}{\varepsilon_{2}}$ કેટલો હશે?View Solution
- 2$196 \,\Omega - 1\,W$ મૂલ્ય ધરાવતા અવરોધના છેડાઓ પર કેટલો મોટો વોલ્ટેજ તમે સલામત રીતે મૂકી શકો ? .......... $volt$View Solution
- 3બે સમાન હિટરના ફિલામેન્ટ, પ્રથમ સમાંતર અને ત્યાર બાદ શ્રેણીમાં જોડવામાં આવે છે.લગાવેલ સમાન વોલ્ટેજ માટે, સમાન સમયમાં, સમાંતર અને શ્રેણી જોડાણોમાં ઉત્પન્ન ઊર્જાનો ગુણોત્તર $.........$ થશે.View Solution
- 4View Solutionછ સમાન અવરોધને પરિપથમાં દર્શાવ્યા પ્રમાણે ગોઠવેલા છે. તો કયા બે બિંદુ વચ્ચેનો સમતુલ્ય અવરોધ મહત્તમ હશે?
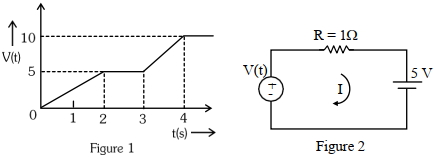
- 5આપેલ પરિપથ માટે ${t}=3.2\, {s}$ સમયે પ્રવાહ ........ ${A}$ હશે.View Solution
[Fig. $(1)$ માં વોલ્ટેજનું વિતરણ અને Fig. $(2)$ માં પરિપથ દર્શાવેલ છે]
- 6$e.m.f.\,\ E$ અને $r$ આંતરિક અવરોધ વાળા બે કોષ અવરોધ $R$ ના બે છેડે સમાંતરમાં જોડેલા છે. જો અવરોધમાનો પાવર મહત્તમ હોય તો...View Solution
- 7એક વાહકનો અવરોધ $15^{\circ} {C}$ એ $16\, \Omega$ અને $100\, ^o{C}$ એ $20\, \Omega$ છે. તો આ વાહકનો તાપમાન અવરોઘક ગુણાંક કેટલો હશે?View Solution
- 8ઘરમાં ઉપયોગમાં લેવાતો સપ્લાI $220 \, V$ નો $9\, ampere$ ના ફયુઝ સાથે છે. તો $60\, W$ ના બલ્બની મહત્તમ સંખ્યા જેમને સમાંતરમાં જોડીને ચાલુ કરી શકાય ?View Solution
- 9$r$ ત્રિજયાવાળા $i$ પ્રવાહધારિત તારમાં ઇલેકટ્રોનનો ડ્રિફટ વેગ $v$ છે, તો સમાન દ્રવ્ય અને અડધી ત્રિજયા ધરાવતા તારમાં $2v$ ડ્રિફટવેગ જોઇતો હોય,તો કેટલો પ્રવાહ પસાર કરવો પડે?View Solution
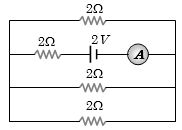
- 10View Solutionઆપેલ પરિપથમાં એમિટરનું અવલોકન શું થાય?