સમાન ચુંબકીય ક્ષેત્ર $B$ માં $r$ ત્રિજ્યાના અર્ધવર્તુળના તારને તેના વ્યાસને અનુલક્ષીને કોણીય આવૃતિ $\omega$ થી ભ્રમણ કરવવામાં આવે છે. પરિભ્રમણની અક્ષ ક્ષેત્રને લંબ છે. જો પરિપથનો કુલ અવરોધ $R$ હોય, તો પરિભ્રમણના સમયગાળા દીઠ ઉત્પન્ન થતો સરેરાશ પાવર કેટલો હશે?
AIEEE 2004, Diffcult
b
Magnetic flux \(=B A \cos \theta=B \cdot \frac{\pi r^{2}}{2} \cos \omega t\)
Magnetic flux \(=B A \cos \theta=B \cdot \frac{\pi r^{2}}{2} \cos \omega t\)
\(\varepsilon_{\text {ind }}=\frac{d \phi}{d t}=\frac{1}{2} B \pi r^{2} \omega \sin \omega t\)
\(P=\frac{\varepsilon_{i n d}^{2}}{R} \frac{B \pi^{2} r^{4} \omega^{2} \sin ^{2} \omega t}{4 R}\)
Now, \(<\sin ^{2} \omega t>=1 / 2\) (mean value)
\(\therefore
=\frac{\left(B \pi r^{2} \omega\right)^{2}}{8 R} \text {. }\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ટ્રાન્સફોર્મરની કાર્યક્ષમતા $80 \%$ અને તે $10 \mathrm{~V}$ અને $4\ \mathrm{KW}$ પર કાર્ય કરે છે. બે ગૌણ ગૂંચળામાં $240 \mathrm{~V}$ હોય તો ગૌણ ગૂંચળામાં પ્રવાહ__________થશે.View Solution
- 2$\oint {\vec B} .d\vec A\, = \,0$ નું કારણ કયું હશે ?View Solution
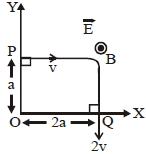
- 3$\mathrm{m}$ દળ અને $q$ વિજભાર ધરાવતો કણ $E\hat{i }$ વિદ્યુતક્ષેત્ર અને $B\hat{k}$ ચુંબકીયક્ષેત્ર ની અંદર બિંદુ $\mathrm{P}$ થી બિંદુ $\mathrm{Q}$ તરફ આકૃતિમાં દર્શાવ્યા પ્રમાણે ગતિ કરે છે. $P$ અને $Q$ બિંદુ આગળ કણનો વેગ અનુક્રમે $v\hat i$ અને $-2 v \hat j$ છે. તો નીચે આપેલા ચાર વિધાન $(\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D})$ માથી ક્યાં સાચા પડે?View Solution
$(A)$ $\mathrm{E}=\frac{3}{4}\left(\frac{\mathrm{mv}^{2}}{\mathrm{qa}}\right)$
$(B)$ $\mathrm{P}$ બિંદુ આગળ વિદ્યુતક્ષેત્રને કારણે થતાં કાર્યનો દર $\frac{3}{4}\left(\frac{\mathrm{mv}^{3}}{\mathrm{a}}\right)$
$(C)$ $\mathrm{Q}$ બિંદુ આગળ બંને ક્ષેત્રને કારણે થતાં કાર્યનો દર શૂન્ય થાય.
$(D)$ $\mathrm{P}$ અને $\mathrm{Q}$ બિંદુ આગળ મળતા કોણીય વેગમાનના મૂલ્યનો તફાવત $2 mav$ થાય.
- 4ટ્રાન્સફોર્મરમાં ગૌણ ગૂંચળામાં આંટાની સંખ્યા અને પ્રાથમિક ગૂંચળામાં આંટાની સંખ્યાનો ગુણોત્તર $5:3$ છે. પ્રાથમિક ગૂંચળામાં વોલ્ટેજ $60 \,V$ છે.,તો ગૌણ ગૂંચળાનો વોલ્ટેજ કેટલા ......$V$ થાય?View Solution
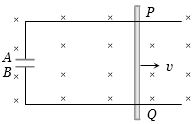
- 5$PQ$ તારની લંબાઇ $1.0\,m$ છે,તેને $4T$ ચુંબકીયક્ષેત્રમાં $2\,m/sec$ ના વેગથી ગતિ કરાવતાં $C = 10 \mu F$ માટે કેપેસીટર પર વિદ્યુતભાર કેટલો થાય?View Solution
- 6$ 20\,\Omega $ અવરોધ ધરાવતી આર્મેચર મોટરને $220 \,V$ $DC$ સપ્લાય સાથે લગાવતાં $1.5 \,A$ નું વહન થાય છે.તો બેક $emf$ કેટલા .......$V$ થાય?View Solution
- 7એક ગુંચળાનું આત્મપ્રેરિત $emf \,25\,V$ છે, જ્યારે તેમાનો પ્રવાહ સમાન દરથી $1 \,s$ માં $10\, A$ થી $25\, A$ કરવામાં આવે છે. ઊર્જામાં થતો ફેરફાર _____$J$ હશે.View Solution
- 8$2\,H$ ઇન્ડકટર અને $10\,\Omega$ અવરોધને શ્રેણીમાં જોડીને $5\,V$ ની બેટરી સાથે જોડતાં શરૂઆતમાં વિદ્યુતપ્રવાહમાં કેટલા .....$amp/sec$ ફેરફાર થાય?View Solution
- 9કોઇલ સાથે સંકળાયેલ ફ્લક્સ ($Wb$) $\phi=5 t^{2}+3 t+16$ દ્વારા દર્શાવવામાં આવે, તો આ કોઇલ સાથે ચોથી સેકન્ડે સંકળાયેલ $emf$ મેળવોView Solution
- 10$10 \mathrm{~cm}$ બાજુ અને $0.7 \Omega$ અવરોધની એક ચોરસ લૂપને પૂર્વ-પશ્રિમ સમતલમાં શિરોલંબ રાખેલી છે.$0.20$$T$ મૂલ્યના સમાન ચુંબકીય ક્ષેત્રને ઉત્તર-પૂર્વ દિશામાંના સમતલમાં રાખેલ છે. ચુંબકીય ક્ષેત્ર $1 S$ માં સ્થિર દરે ધટીને શૂન્ય થાય છે. તો પ્રેરિત emf નું મૂલ્ય $\sqrt{x} \times 10^{-3} V$ છે. તો $x$ નું મૂલ્ય________છે.View Solution
