In uniform magnetic field,
\(\mathrm{R}=\frac{\mathrm{m} v}{\mathrm{qB}}=\frac{\sqrt{2 \mathrm{~m}(\mathrm{~K} \cdot \mathrm{E})}}{\mathrm{qB}}\)
Since same \(K.E\)
\(\mathrm{R} \propto \frac{\sqrt{\mathrm{m}}}{\mathrm{q}}\)
\(\therefore \frac{\mathrm{R}_{\text {deutron }}}{\mathrm{R}_{\text {proton }}}=\sqrt{\frac{\mathrm{m}_{\mathrm{d}}}{\mathrm{m}_{\mathrm{p}}}} \times \frac{\mathrm{q}_{\mathrm{p}}}{\mathrm{q}_{\mathrm{d}}}\)
\(=\sqrt{2} \times 1\)
\(\therefore \gamma_{\mathrm{d}}: \gamma_{\mathrm{p}}=\sqrt{2}: 1\)
Download our appand get started for free
Similar Questions
- 1$4 \pi$ મીટર લંબાઈના તારને વાળીને $6$ બાજુઓ વાળો બહુકોણ (ષટ્કોણ) બનાવવામાં આવે છે. જો બહુકોણ $4 \pi \sqrt{3} \mathrm{~A}$ વિદ્યુત્પવાહનું વહન કરતો હોય તો બહુકોણના કેન્દ્ર પરનું ચુંબકીય ક્ષેત્ર $10^{-7} x$ ટેસ્લા છે. $x$ નું મૂલ્ય____________છે.View Solution
- 2એક પ્રોટોન, એક ડયુટેરોન અને એક $\alpha -$ કણ સમાન ચુંબકીય ક્ષેત્રમાં સમાન વેગમાન સાથે ગતિ કરે છે. તેમના પર લાગતા ચુંબકીય બળોનો અને તેમની ઝડપનો ગુણોત્તર, આપેલ ક્રમમાં, અનુક્રમે .......... અને ........... છે.View Solution
- 3નીચે બે વિધાનો આપેલા છે.View Solution
વિધન $I:$ ચલિત ગૂંચળાવાળા ગેલ્વેનોમીટરમાં ગૂંચળાના આંટાની સંખ્યા બમણી કરતાં તેની પ્રવાહ સંવેદિતા બમણી થાય.
વિધન $II$ : ફક્ત ગૂંચળાના આંટાની સંખ્યા વધારીને ચલિત ગૂંયળાવાળા ગેલ્વેનીમીટર પ્રવાહ સંવેદિતા વધારતા તેની વોલ્ટેજ સંવેદિતા પણ તેટલા જ ગુણોત્તર પ્રમાણે વધશે.
ઉપર્યુક્ત કથનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાયો ઉત્તર પસંદ કરો.
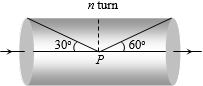
- 4આપેલ આકૃતિમાં $P $ બિંદુએ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 5વર્તુળાકાર ગુંચળાની અક્ષ પર કેન્દ્રથી અનુક્રમે $0.05\, m$ અને $0.2\, m$ અંતરે રહેલ બે બિંદુઓ આગળ ચુંબકીય ક્ષેત્રો $8:1$ નાં ગુણોત્તરમાં છે. ગુંચળાની ત્રિજ્યા ........... $m $ છે.View Solution
- 6આકૃતિમાં બતાવ્યા પ્રમાણે પેપરના સમતલમાં એક અનંત લંબાઇના વિદ્યુત પ્રવાહ ધારીત તાર અને નાનો પ્રવાહ ધારિત ગોળો આપેલ છે. ગોળાની ત્રિજ્યા $a$ છે અને તેના કેન્દ્રથી તાર સુધીનું અંતર $d, (d > > a)$ છે. જો ગોળો તાર પર $F$ બળ લગાવે તોView Solution
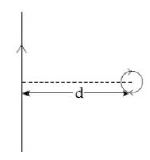
- 7નીચેની આકૃતિમાં $P$ બિંદુ આગળ ચુંબકીયક્ષેત્રનો ગુણોત્તર કેટલો થાય?View Solution
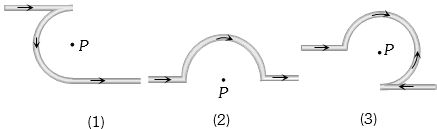
- 8આપેલ તંત્રમાં $Q$ તારની લંબાઇ $10\,cm$ હોય,તો તેના પર કેટલું બળ લાગે?View Solution
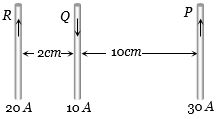
- 9પ્રોટોન,ઇલેક્ટ્રોન અને હીલિયમ ન્યુક્લિયસ પાસે સમાન ઉર્જા છે.તેના સમતલને લંબ ચુંબકીય ક્ષેત્રને કારણે તે વર્તુળાકાર કક્ષામાં ભ્રમણ કરે છે.તેમની ત્રિજ્યા અનુક્રમે $r_p, r_e$ અને $r_{He}$ હોય તો....View Solution
- 10View Solutionનીચેનામાંથી ક્યું વાક્ય મુજબ ચુંબકીય બળ રેખાનાં સંદર્ભે સાચી છે ?
