સમાન જાડાઇ ધરાવતા બે સ્તરો $A$ અને $B$ ની દીવાલ બનેલી છે.$A$ ની ઉષ્માવાહકતા $B$ કરતાં બમણી છે.દીવાલના બંને છેડા વચ્ચે તાપમાનનો તફાવત $ {36^o}C $ છે.તો $A$ સ્તર વચ્ચે તાપમાન તફાવત ..... $^oC$ હશે?
IIT 1980, Diffcult
b
(b) Suppose thickness of each wall is \(x\) then \({\left( {\frac{Q}{t}} \right)_{combination}} = {\left( {\frac{Q}{t}} \right)_A}\)
(b) Suppose thickness of each wall is \(x\) then \({\left( {\frac{Q}{t}} \right)_{combination}} = {\left( {\frac{Q}{t}} \right)_A}\)
==> \(\frac{{{K_S}A({\theta _1} - {\theta _2})}}{{2x}} = \frac{{2KA({\theta _1} - \theta )}}{x}\)
\(\because {K_S} = \frac{{2 \times 2K \times K}}{{(2K + K)}} = \frac{4}{3}K\) and \(({\theta _1} - {\theta _2}) = 36^\circ \)
==> \(\frac{{\frac{4}{3}KA \times 36}}{{2x}} = \frac{{2KA({\theta _1} - \theta )}}{x}\)
Hence temperature difference across wall \(A\) is \(({\theta _1} - \theta ) = {12^o}C\)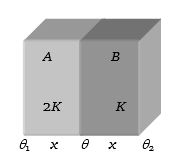
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$T K$ તાપમાને રહેલ પદાર્થમાંથી ઉત્સર્જન પાવર $E\, W/m^2$ છે,તો $ \frac{T}{2}K $ તાપમાને રહેલ તે જ પદાર્થનો ઉત્સર્જન પાવર કેટલો થાય?View Solution
- 2બે સમાન ક્ષેત્રફળ વાળી પ્લેટને એકબીજાના સંપર્કમાં રાખેલી છે. તેમની જાડાઈ $2.0\,\, cm$ અને $5.0 \,\,cm$ છે. પહેલી પ્લેટની બાહ્ય સપાટીનું તાપમાન $-20°C$ અને બીજી પ્લેટની બાહ્ય સપાટીનું તાપમાન $20°C$ છે. જ્યારે તેમની ઉષ્મા વાહકતાનો ગુણોત્તર $2:5$ હોય તો સંપર્કમાં રહેલી સપાટીનું તાપમાન ........ $^oC$ શોધો.View Solution
- 3કોપર,બ્રાસ અને સ્ટિલના ત્રણ સળિયાને $Y-$ આકારની સંરચના કરવા માટે વેલ્ડિંગ કરવામાં આવે છે.દરેક સળિયાના આડછેદનું ક્ષેત્રફળ $4 $ $cm^2$ છે.કોપર સળિયાના છેડે $100^o $ $C$ તાપમાન જયારે બ્રાસ અને સ્ટિલ સળિયાઓને છેડે $ 0^o $ $C$ તાપમાન જાળવવામાં આવે છે.કોપર,બ્રાસ અને સ્ટિલના સળિયાઓની લંબાઇ અનુક્રમે $46,13 $ અને $12$ cms છે. આ સળિયાઓ છેડેથી જ તાપમાનના સુવાહક છે.જયારે આજુબાજુથી અવાહક છે.કોપર,બ્રાસ અને સ્ટિલની ઉષ્મા વાહકતા અનુક્રમે $0.92,0.26 $ અને $ 0.12 $ $CGS $ એકમમાં છે.કોપર સળિયામાંથી પસાર થતો ઉષ્મા વહન-દર ....... $cal\, s^{-1}$View Solution
- 4કાળો પદાર્થ $5760\; K$ તાપમાને છે. આ પદાર્થ દ્વારા ઉત્સર્જિત વિકિરણની ઊર્જા $250\,nm$ તરંગલંબાઇ પર $U _{1}$, $500\,nm$ તરંગલંબાઇ પર $U _{2}$ અને $1000\,nm$ તરંગલંબાઇ પર $U _{3}$ છે. વીન અચળાંક $b= 2.88 \times 10^6 \;nm-K $ છે. નીચેનામાંથી કયો સંબંધ સાચો છે?View Solution
- 5$127°C$ એ કાળા પદાર્થમાંથી $1.0 × 10^{6} J/sm^{2} $ ના દરથી ઉર્જાનું ઉત્સર્જન થાય છે. કયા તાપમાને ઉર્જાનું ઉત્સર્જન $16.0 ×10^{6} J/sm^{2}$ .....$^oC$ થશે.View Solution
- 6સૂર્યમાંથી નીકળતી ઊર્જાએ પૃથ્વીની સપાટી પર $20\, \frac{{kcal}}{{{m^2}\;min}}$ ના દરે લંબ રૂપે આપાત થાય છે. જો સૂર્યનું તાપમાન અત્યાર કરતાં બમણું થાય, તો પૃથ્વીની સપાટી પર લંબરૂપે આપાત થતી ઉત્સર્જન ઊર્જા ($kcal/m ^2 \,min$ માં) કેટલી થાય?View Solution
- 7ઉષ્મીય રીતે અલગ કરેલા એક સળિયાનાં બંને છેડાનાં તાપમાનો અનુક્રમે $T _{1}$ અને $T _{2}$ છે. સળિયો $l_{1}$ અને $l_{2}$ એમ બે વિભાગોના જોડાણથી બનેલો છે. બંને દ્રવ્યોની ઉષ્માવાહકતા $k _{1}$ અને $k _{2}$ છે. તો બે ભાગોની જોડતી સપાટીએ તાપમાન કેટલું થાય?View Solution

- 8બ્રાસ અને સ્ટીલના તારના રેખીય પ્રસરણાંક ${\alpha _1}$ અને ${\alpha _2}$ છે,તેમની $0°C$ તાપમાને લંબાઇ ${l_1}$ અને ${l_2}$ છે.જો કોઇપણ તાપમાને $({l_2} - {l_1})$ અચળ રહેતું હોય,તોView Solution
- 9જો ધાતુની પટ્ટી કે જેને ત્રીજ્યા $r$ અને $2 r$ છે તે તાપીય રેડીયેશન તેની મહત્તમ તરંગલંબાઈ તીવ્રતા $\lambda$ અને $2 \lambda$ છે. તો તેની ક્રમશ રેડીયેશન ઉર્જા/સેકન્ડનો ગુણોત્તર કેટલો હશે ?View Solution
- 10જો સૂર્યની ત્રિજયા $100$ ગણી અને તાપમાન અડધું કરવામાં આવે,તો ઉત્સર્જન ઊર્જા કેટલા ગણી વધે?View Solution
