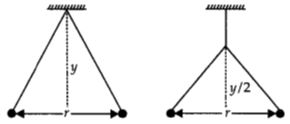
Let \(m\) be mass of each ball and \(q\) be charge on each ball. Force of repulsion
\(F=\frac{1}{4 \pi \varepsilon_{0}} \frac{q^{2}}{r^{2}}\)
In equilibrium
\(T \cos \theta=m g\) \(...(i)\)
\(T \sin \theta=F\) \(...(ii)\)
Divide \((ii)\) by \((i),\) we get,
\(\tan \theta=\frac{F}{m g}=\frac{\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}}}{m g}\)
From figure \((a),\)
\(\frac{r / 2}{y}=\frac{\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}}}{m g}\) \(....(iii)\)
\(\tan \theta^{\prime}=\frac{\frac{1}{4 \pi \varepsilon_{0}} \frac{q^{2}}{r^{\prime 2}}}{m g}\)
From figure \((b)\)
\(\frac{r^{\prime} / 2}{y / 2}=\frac{\frac{1}{4 \pi \varepsilon_{0}} \frac{q^{2}}{r^{\prime 2}}}{m g} \ldots(\mathrm{iv})\)
Divide \((iv)\) by \((iii),\) we get
\(\frac{2 r^{\prime}}{r}=\frac{r^{2}}{r^{\prime 2}} \Rightarrow r^{\prime 3}=\frac{r^{3}}{2}\)
\(\Rightarrow r^{\prime}=\frac{r}{\sqrt[3]{2}}\)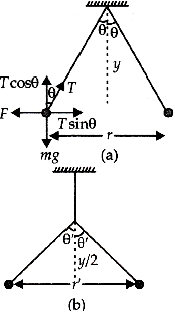
Download our appand get started for free
Similar Questions
- 1$20$ યુનિટ ક્ષેત્રફળ ધરાવતી સપાટી $Y-Z$ સમતલમાં છે,જો વિદ્યુતક્ષેત્ર $(5 \hat{i}+4 \hat{j}+9 \hat{k})$ હોય તો સપાટીમાંથી પસાર થતું ફલક્સ શોધો. (એકમ માં)View Solution
- 2$h$ ઊંચાઈ અને $R$ બેજની ત્રિજ્યા ધરાવતા શંકુને $\vec E$ વિદ્યુતક્ષેત્રમાં એવી રીતે મૂકવામાં આવે છે કે જેથી વિદ્યુતક્ષેત્ર બેજને સમાંતર રહે.તો શંકુમાં દાખલ થતું વિદ્યુત ફ્લક્સ કેટલું હશે?View Solution
- 3View Solutionઈલેકટ્રોન અને પ્રોટોન સમાન વિદ્યુતક્ષેત્રમાં મૂકેલા છે. તેઓના પ્રવેગનો ગુણોત્તર ...... છે.
- 4સમાન $m$ દળ અને સમાન વિદ્યુતભાર $q$ ને $16\, cm$ અંતરે રહેલા છે.તે બંને પર લાગતું બળ શૂન્ય હોય,તો $\frac{q}{m} =$ ______View Solution
- 5મુક્ત અવકાશમાં $z-$અક્ષ પર $8\, nC / m$ ના સમાંગ રેખીય વિદ્યુતભાર ધરાવતાં વિસ્તરમાં $x =3\, m$ બિંદુ આગળ વિદ્યુત ફલક્સ ઘનતા શોધો :View Solution
- 6$1.2 \times 10^{-30} \,Cm$ અને $2.4 \times 10^{-30} \,Cm$ દ્વિ-ધ્રુવી ચાકમાત્રા ધરાવતી બે વિદ્યુત દ્વિ-ધ્રુવીઓને અનુક્રમે બે $5 \times 10^{4}$ $NC ^{-1}$ અને $15 \times 10^{4} \,NC ^{-1}$ જેટલા નિયમીત વિદ્યુતક્ષેત્રમાં મૂકવામાં આવે છે. વિદ્યુત દ્વિ-ધુવીઓ દ્વારા અનુભવતા મહત્તમ ટોર્કનો ગુણોત્તર $\frac{1}{x}$ છે. $x$ નું મૂલ્ય ......... થશે.View Solution
- 7$ + 4q,\, - q$ અને $ + 4q$ વિદ્યુતભાર ધરાવતા બિંદુવત વિદ્યુતભારને $x - $અક્ષ પર $x = 0,\,x = a$ અને $x = 2a$ પર મૂકવામાં આવે તો ...View Solution
- 8View Solutionકુલંબના નિયમ પ્રમાણે નીચેની આકૃતિ માટે શું સાયું છે ?

- 9સમાન મૂલ્ય $0.01\,C$ ના અને $0.4\,mm$ અંતરે રાખેલા બે વિદ્યુતભારો, વિદ્યુત ડાયપોલ (દ્વિધ્રુવી) ની રચના કરે છે. જો દ્રી-ધ્રુવીને $10\,dyne/C$ ના નિયમિત વિદ્યુતક્ષેત્ર $\vec{E}$ માં, $\vec{E}$ સાથે $30^{\circ}$ ના કોણે મૂકવામાં આવે, તો દ્વિ-ધ્રુવી પર લાગતા ટોર્કનું મૂલ્ય ...... હશે.View Solution
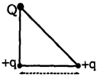
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે બે બાજુઓ સમાન હોય તેવા કાટકોણ ત્રિકોણના શિરોબિંદુઓ આગળ ત્રણ વિદ્યુતભાર $Q, +q$ અને $+q$ મૂકેલા છે. તંત્રની રચનાનું ચોખ્ખું સ્થિત વિદ્યુત શાસ્ત્રનું બળ શૂન્ય છે. જો $Q$ ........ ને સમાન છે.View Solution