જ્યારે \(\vec A \) અને \(\vec B \) સમાંતરબાજુ ચતુષ્કોણના વિકર્ણ હોય ત્યારે સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ \( = \frac{1}{2} |\mathop A\limits^ \to \times \mathop B\limits^ \to | \)
\({\mathop {{\rm{ }}A}\limits^ \to \times \mathop {{\rm{ }}B}\limits^ \to = \left| {\left. {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k}\\ 5&{ - 4}&3\\ 3&{ - 2}&{ - 1} \end{array}} \right|} \right.}\) \({ = i\left| {\left. {\begin{array}{*{20}{c}} { - 4}&3\\ { - 2}&{ - 1} \end{array}} \right| - j\left| {\left. {\begin{array}{*{20}{c}} 5&3\\ 3&{ - 1} \end{array}} \right|} \right.} \right. + k\left| {\left. {\begin{array}{*{20}{c}} 5&{ - 4}\\ 3&{ - 2} \end{array}} \right|} \right.}\)
\( = \frac{1}{2}|\mathop {{\rm{ }}A}\limits^ \to \times \mathop {{\rm{ }}B}\limits^ \to |=\) \({\hat i\left\{ {\left. {\left( { - 4} \right)\left( { - 1} \right) - \left( 3 \right)\left( { - 2} \right)} \right\}} \right. - \hat j\left\{ {\left. {\left( 5 \right)\left( { - 1} \right) - \left( 3 \right)\left( 3 \right)} \right\} + \hat k\left\{ {\left. {\left( 5 \right)\left( { - 2} \right) - \left( { - 4} \right)\left( 3 \right)} \right\}} \right.} \right.}\) \({ = 10\hat i + 14\hat j + 2\hat k}\) \({|\mathop A\limits^ \to \times \mathop B\limits^ \to | = \sqrt {{{\left( {10} \right)}^2} + {{\left( {14} \right)}^2} + {{\left( 2 \right)}^2}} = \sqrt {300} }\)
\(\frac{1}{2} |\mathop A\limits^ \to \times \mathop B\limits^ \to | \Rightarrow \frac{1}{2} \times 10\sqrt 3 = 5\sqrt 3 \)
Download our appand get started for free
Similar Questions
- 1View Solutionઅલગ અલગ સમતલના કેટલા સદિશોનો સરવાળો કરતાં પરિણામી શૂન્ય મળે ?
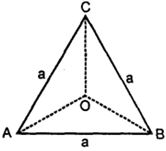
- 2$ABC$ એ સમબાજુ ત્રિકોણ છે. દરેક બાજુની લંબાઈ $'a'$ અને તેનું પરિકેન્દ્ર $O$ છે. તો $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=.......$View Solution
- 3જો $\mathop {\text{A}}\limits^ \to $ અને $\mathop {\text{B}}\limits^ \to $ વચ્ચેનો ખૂણો $\theta$ હોય તો, $\left( {\mathop {\text{B}}\limits^ \to \,\, \times \,\,\mathop {\text{A}}\limits^ \to } \right)\,\,.\,\,\mathop {\text{A}}\limits^ \to \,\,$ ગુણાકારની કિંમત કોને સમાન થાય છે ?View Solution
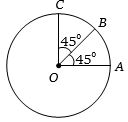
- 4જો વર્તુળની ત્રિજયા $R$ હોય તો સદિશો $ \overrightarrow {OA} ,\,\overrightarrow {OB} $ અને $ \overrightarrow {OC} $ નો પરિણામી સદિશ કેટલો થશે?View Solution
- 5જો $\,{\rm{|}}\mathop {\rm{A}}\limits^ \to \,\, + \;\,\mathop B\limits^ \to \,|\,\, = \,\,\,{\rm{|}}\mathop {\rm{A}}\limits^ \to \,\, - \;\,\mathop B\limits^ \to \,|\,$ હોય $\vec A $ અને $\vec B $ વચ્ચેનો ખૂણો ........ $^o$View Solution
- 6કાર્તેઝિયન યામ પદ્ધતિમાં સદિશોView Solution
$ \vec a = 4\hat i - \hat j $ , $ \vec b = - 3\hat i + 2\hat j $ અને $ \vec c = - \hat k $ છે.
જ્યાં $\hat i,\,\hat j,\,\hat k$ એ અનુક્રમે $X,Y,Z$ ની દિશામાનો એકમ સદીશ છે તો તેના પરિણામી સદિશની દિશામાંનો એકમ સદિશ $\hat r$ શું મળે ?
- 7જો $ |\vec A \times \vec B| = \sqrt 3 \vec A.\vec B $ હોય, તો $ |\vec A + \vec B| $ નું મૂલ્ય શું થાય?View Solution
- 8સદિશ $\overrightarrow {\rm A} = 2\hat i + 3\hat j - \hat k$નો સદિશ $\overrightarrow B = - \hat i + 3\hat j + 4\hat k$ ની દિશામાંનો પ્રક્ષેપ મેળવો.View Solution
- 9વિધાન $I :$ બે બળો $(\overrightarrow{{P}}+\overrightarrow{{Q}})$ અને $(\overrightarrow{{P}}-\overrightarrow{{Q}})$, જ્યાં $\overrightarrow{{P}} \perp \overrightarrow{{Q}}$, જ્યારે આ બંને બળો એકબીજા સાથે $\theta_{1}$ ખૂણે હોય ત્યારે તેનું પરિણામી બળ $\sqrt{3\left({P}^{2}+{Q}^{2}\right)}$ મળે, જ્યારે આ બંને બળો એકબીજા સાથે $\theta_{2}$ ખૂણે હોય, ત્યારે તેનું પરિણામી $\sqrt{2\left({P}^{2}+{Q}^{2}\right)}$ મળે છે. આ માત્ર $\theta_{1}<\theta_{2}$ માટે શક્ય છે.View Solution
વિધાન $II :$ ઉપર આપેલ પરિસ્થિતીમાં $\theta_{1}=60^{\circ}$ અને $\theta_{2}=90^{\circ}$ હોય.
આપેલ વિધાનોમાંથી સૌથી યોગ્ય જવાબ પસંદ કરો.
- 10જો $ \overrightarrow A \times \overrightarrow B = \overrightarrow C , $ તો નીચેનામાંથી કયું વિધાન ખોટું છે?View Solution
