As \(\mathrm{K}\) is variable we take a plate element of Area \(A\) and thickness \(dx\) at distance \(\mathrm{x}\)
Capacitance of element
\(\mathrm{d} \mathrm{C}=\frac{(\mathrm{A}) \mathrm{K}(1+\alpha \mathrm{x}) \varepsilon_{0}}{\mathrm{dx}}\)
Now all such elements are is series so
equivalent capacitance
\(\frac{1}{\mathrm{C}}=\int \frac{1}{\mathrm{d} \mathrm{C}}=\int_{0}^{\mathrm{d}} \frac{\mathrm{dx}}{\mathrm{AK} \varepsilon_{0}(1+\alpha \mathrm{x})}\)
\(\frac{1}{\mathrm{C}}=\frac{1}{\alpha \mathrm{AK} \varepsilon_{0}} \ln \left(\frac{1+\alpha \mathrm{d}}{1}\right)\)
\(=\frac{1}{\mathrm{C}}=\frac{1}{\alpha \mathrm{AK} \varepsilon_{0}}\left(\alpha \mathrm{d}-\frac{(\alpha \mathrm{d})^{2}}{2}+\frac{(\alpha \mathrm{d})^{3}}{3}+\ldots .\right)\)
\(\Rightarrow \frac{1}{\mathrm{C}}=\frac{\alpha \mathrm{d}}{\alpha \mathrm{AK} \varepsilon_{0}}\left(1-\frac{\alpha \mathrm{d}}{2}+\frac{(\alpha \mathrm{d})^{2}}{3}+\ldots .\right)\)
\(\frac{1}{\mathrm{C}}=\frac{\mathrm{d}}{\mathrm{AK} \varepsilon_{0}}\left(1-\frac{\alpha \mathrm{d}}{2}\right)\)
\(C=\frac{A K \varepsilon_{0}}{d}\left(1+\frac{\alpha d}{2}\right)\)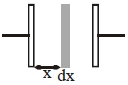
Download our appand get started for free
Similar Questions
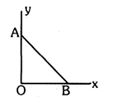
- 1આ આલેખ પરથીએક બિંદુવત વિદ્યુતભાર $+q$ ને ઉગમબિંદુ આગળ મૂકેલો છે. બીજા બિંદુવત વિદ્યુતભાર $-Q$ ને સુરેખ પથ $AB$ પર બિંદુ $A$ ના યામ $(0, a)$ ન થી બિંદુ $B$ ના યામ $(a, 0)$ ન સુધી લઈ જતાં થતુ કાર્ય ....... છે.View Solution
- 2$5.0\, \mu F$ કેપેસિટરને $800\, V$ સુધી ચાર્જ કરીને વાહક સાથે જોડતા ડિસ્ચાર્જ દરમિયાન વાહકને આપેલ ઊર્જા .....View Solution
- 3નિયમિત વિદ્યુતક્ષેત્ર $\vec E, \,X-$ દિશામાંં છે. $0.2\;C$ વિદ્યુતભારને $x-$દિશા સાથે $60^\circ $ના ખૂણે $2 \,m$ જેટલું સ્થાનાંતર કરાવવા માટે $4\;J$ કાર્ય કરવું પડે છે, તો વિદ્યુતક્ષેત્ર $E$ કેટલા.......$N/C$ થાય?View Solution
- 4કોઈ સમાંતર પ્લેટ કેપેસિટરની દરેક પ્લેટનું ક્ષેત્રફળ $1\, m^2$ અને તેમની વચ્ચેનું અંતર $0.1\, m$ છે. જો બે પ્લટો વચ્ચેનું વિદ્યુત ક્ષેત્ર $100 \,N/C$ હોય તો દરેક પ્લેટ પરના વિધુતભારનું મૂલ્ય કેટલું થશે?View Solution
- 5$2\mu F$ કેપેસિટેન્સ ધરાવતા સાત કેપેસિટરોને એવી સંરચના વડે જોડવામાં આવે છે કે જેથી તેનો અસરકારક કેપેસિટન્સ $\left( {\frac{6}{{13}}} \right)\,\mu F$ મળે. નીચેની આકૃતીમાંથી ક્યું સંયોજન જરૂરી મૂલ્ય આપે છે?View Solution
- 6View Solutionવિદ્યુતભારિત વાહક ગોળા માટે કયું વિધાન સાચું નથી?
- 7$a$ બાજુવાળા ચોરસના શિરોબિંદુ પર $Q$ વિજભાર મૂકવામાં આવે છે. ચોરસના કેન્દ્રથી $-Q$ વિજભારને અનંત અંતરે લઈ જવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 8બે સમકેન્દ્રિય ગોળીય કવચથી કેપેસિટર બનાવવામાં આવે છે, ${R_1}$ ત્રિજયાવાળી ગોળીય કવચનો વોલ્ટેજ ${V_1}$ અને ${R_2}$ ત્રિજયાવાળી ગોળીય કવચનો વોલ્ટેજ ${V_2}$ છે,તો કેન્દ્રથી $x$ અંતરે આવેલા બિંદુએ વોલ્ટેજ કેટલો થાય? (${R_2} > x > {R_1}$)View Solution
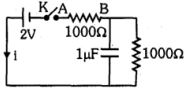
- 9$t = 0$ સમયે જ્યારે કળને દબાવવામાં આવે છે ત્યારે આપેલા પરિપંથમાં $AB$ અવરોધમાંના $'i'$ વિદ્યુતપ્રવાહ માટે નીચેનામાંથી કયું વિધાન સાચું છે ?View Solution
- 10બે ગોળાકાર તકતીઓને $5$ $mm $ અંતરે રાખી તેમની વચ્ચે $2.2$ ડાયઇલેકિટ્રક અચળાંક ધરાવતો અવાહક મૂકો.એક સમાંતર પ્લેટ કેપેસિટરર્સ બનાવવામાં આવે છે.જયારે અવાહકનું વિદ્યુતક્ષેત્ર $3 \times 10^4$ $ Vm^{-1}$ હોય,ત્યારે ધન પ્લેટ (તકતી) ની વિદ્યુતભાર ઘનતા લગભગ _______ હશે.View Solution
