for first lens \(=\frac{1}{v_{1}}-\frac{1}{-x}=\frac{1}{1} \Rightarrow v_{1}=\frac{x}{x-1}\)
also magnification \(\left| m _{1}\right|=\left|\frac{ v _{1}}{ u _{1}}\right|=\frac{1}{ x -1}\)
for \(2^{nd}\) lens this is acting as object
so \(u _{2}=-\left(20- v _{1}\right)=-\left(20-\frac{ x }{ x -1}\right)\)
and \(v _{2}=-25 cm\)
angular magnification \(\left| m _{ A }\right|=\left|\frac{ D }{ u _{2}}\right|=\frac{25}{\left| u _{2}\right|}\)
Total magnification \(m = m _{1} m _{ A }=100\)
\(\left(\frac{1}{x-1}\right)\left(\frac{25}{20-\frac{x}{x-1}}\right)=100\)
\(\frac{25}{20(x-1)-x}=100 \Rightarrow 1=80(x-1)-4 x\)
\(\Rightarrow 76 x=81 \Rightarrow x=\frac{81}{76}\)
\(\Rightarrow u _{2}=-\left(20-\frac{81 / 76}{81 / 76-1}\right)=\frac{-19}{5}\)
now by lens formula
\(\frac{1}{-25}-\frac{1}{-19 / 5}=\frac{1}{f_{e}} \Rightarrow f_{e}=\frac{25 \times 19}{106} \approx 4.48 cm\)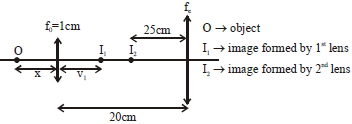
Download our appand get started for free
Similar Questions
- 1View Solutionઓરડાની છત અને બે પાસપાસેની દીવાલ પર અરીસા હોય,તો ઓરડા રહેલ માણસના કેટલા પ્રતિબિંબ દેખાય?
- 2કાટખૂણો ધરાવતા પ્રિઝમની એક બાજુને લંબ રૂપે પ્રકાશ આપાત કરતાં તે પ્રિઝમમાં પાયાને સમાંતર ગતિ કરે છે. જો પ્રિઝમનો વક્રીભવનાંક $\mu$ હોય,તો કર્ણએ પાયા સાથે બનાવેલ ખૂણો કેટલો રાખવાથી કિરણ કર્ણ દ્વારા સંપૂર્ણ પરાવર્તન પામે?View Solution
- 3સંયુક્ત માઇક્રોસ્કોપના વસ્તુકાંચ અને નેત્રકાંચની કેન્દ્રલંબાઈ અનુક્રમે $1.2\, cm$ અને $3.0\, cm$ છે. જો વસ્તુને વસ્તુકાંચથી $1.25\, cm$ અંતરે મૂકવામાં આવે તો અંતિમ પ્રતિબિંબ અનંત અંતરે મળે છે. તો આ સંયુક્ત માઇક્રોસ્કોપની મોટવણી કેટલી હશે?View Solution
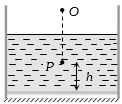
- 4તળિયે સમતલ અરીસો ધરાવતા પાત્રમાં $\mu $ વક્રીભવનાંક ધરાવતું પ્રવાહી ભરેલ છે. અરીસાથી $h$ ઊંચાઇ ઉપર $P$ વસ્તુને અવલોકનકાર $O$ જોવે છે. તો વસ્તુ અને પ્રતિબિંબ વચ્ચેનું અંતર કેટલું થાય?View Solution
- 5પ્રિઝમ $(\mu = 1.5)$ નો પ્રિઝમકોણ $30^°$ છે.એક સપાટીને લંબ કિરણ આપાત કરતાં તેનું વિચલન કેટલું થાય? ($sin 48^° 36’ = 0.75$)View Solution
- 6લઘુ દ્રષ્ટિને દૂર કરવા $0.66 D $ પાવરનો લેન્સ વપરાય છે. તો આંખનો દૂર સૌથી દૂરનું બિંદુ .......$cm$ થશે.View Solution
- 7$P$ બિંદુ એ પ્રકાશ કિરણ પુંજ અભિકેન્દ્રીત થાય છે. $P$ બિંદુથી $12\,\, cm$ પ્રકાશ પુંજના પથ પર એક લેન્સ મૂકવામાં આવે છે. જો લેન્સ $16\,\, cm$ કેન્દ્રલંબાઈ ધરાવતો અંતર્ગોળ કાચ હોય, તો ક્યાં......$cm$ બિંદુએ કિરણપુંજ અભિકેન્દ્રિત થાય?View Solution
- 8માછલી ઘરમાં પાણીની સપાટીથી $30\,cm$ ઊંડાઈએ રહેલી માછલી પાણીની સપાટી થી $50\,cm$ ઊંચાઈએ રહેલા બલ્બને જોઈ શકે છે. આ માછલી બલ્બનું પ્રતિબિંબ પણ જોઈ શકે છે. પાણીની કુલ ઊંડાઈ $60\,cm$ છે. માછલી ને દેખાતા બન્ને પ્રતિબિંબ વચ્ચેનું અંતર.View Solution
- 9$f$ કેન્દ્રલંબાઇ ઘરાવતા અંર્તગોળ અરીસાની અક્ષ પર $f/3$ લંબાઇની વસ્તુ મૂકવામાં આવે છે. તેના અરીસાથી દૂરના છેડાનું પ્રતિબિંબ તે જ જગ્યાએ મળે છે,તો પ્રતિબિંબની લંબાઇ કેટલી થાય?View Solution
- 10ઓબ્જેકિટવ અને આઇપીસની કેન્દ્રલંબાઇ $1 \,cm$ અને $5\, cm $ છે,મોટવણી $45$ હોય,તો ટયુબ લંબાઇ કેટલા .....$cm$ થાય?View Solution
