સંયુક્ત માઇક્રોસ્કોપના વસ્તુકાંચ અને નેત્રકાંચની કેન્દ્રલંબાઈ અનુક્રમે $1.2\, cm$ અને $3.0\, cm$ છે. જો વસ્તુને વસ્તુકાંચથી $1.25\, cm$ અંતરે મૂકવામાં આવે તો અંતિમ પ્રતિબિંબ અનંત અંતરે મળે છે. તો આ સંયુક્ત માઇક્રોસ્કોપની મોટવણી કેટલી હશે?
JEE MAIN 2014, Diffcult
a
Given \(: f_{0}=1.2\, \mathrm{cm} ; f_{\mathrm{e}}=3.0 \,\mathrm{cm}\)
Given \(: f_{0}=1.2\, \mathrm{cm} ; f_{\mathrm{e}}=3.0 \,\mathrm{cm}\)
\(u_{0}=1.25\, \mathrm{cm} ; M_{\infty}=?\)
From \(\frac{1}{f_{0}}=\frac{1}{v_{0}}-\frac{1}{u_{0}}\)
\(\Rightarrow \frac{1}{1.2}=\frac{1}{v_{0}}-\frac{1}{(-1.25)}\)
\(\Rightarrow \quad \frac{1}{v_{0}}=\frac{1}{1.2}-\frac{1}{1.25}\)
\(\Rightarrow \) \(v_{0}=30\, \mathrm{cm}\)
Magnification at infinity,
\(M_{\infty}=-\frac{v_{0}}{u_{0}} \times \frac{D}{f_{e}}\)
\(=\frac{30}{1.25} \times \frac{25}{3}\) ( \(\because D=25\, \mathrm{cm}\) least distance of distinct vision)
\(=200\)
Hence the magnifying power of the compound microscope is \(200\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ગુરુદ્રષ્ટિની ખામી ધરાવતો માણસ $120\,\, cm$ થી નજીકની વસ્તુ પર ધ્યાન કેન્દ્રિત કરી શકતો નથી. લેન્સ દ્વારા તે $40 \,\,cm$ અંતરે સુધી વાંચી શકે છે તો કેન્દ્રલંબાઈ ......$cm$ છે.View Solution
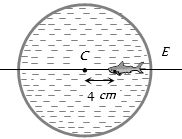
- 2$10\, cm $ ત્રિજ્યાના ગોળાકાર પાત્રને $(4/3)$ વક્રીભવનાંક વાળા પાણીથી ભરેલું છે. આકૃતિમાં બતાવ્યા પ્રમાણે કેન્દ્ર $C$ થી $4 \,cm$ ના અંતરે એક માછલી છે. જો છેડા $E$ થી જોવામાં આવે તો માછલી ......$cm$ દેખાતી હશે? (માછલી જોડાઈ અવગણતાં)View Solution
- 3ટેલિસ્કોપની ઓબ્જિેકિટવપીસ અને આઇપીસની કેન્દ્રલંબાઇ $0.3m$ અને $0.05m$ છે.તો બંને લેન્સ વચ્ચેનું અંતર.....$m$View Solution
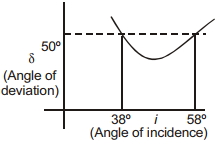
- 4View Solutionઆકૃતિમાં વિચલનકોણ અને આપાતકોણ વચ્ચેનો આલેખ દર્શાવેલ છે. આલેખ પરથી કહી શકાય કે પ્રિઝમકોણ કેટલો છે?
- 5પ્રકાશનું કિરણ ધટ્ટ માધ્યમમાંથી પાતળા માધ્યમમાં ગતિ કરે છે. તેના માટે ક્રાંતિકોણ $C$ છે,તો કિરણનું મહત્તમ વિચલન કેટલું થાય?View Solution
- 6બે $40°$ ખૂણે રહેલા અરીસા દ્વારા કિરણનું સફળતાથી પરાવર્તન થાય છે. જો પ્રથમ અરીસા પર આપાત કોણ $30°$ હોય ત્યારે કિરણનું કુલ વિચલન .....$^o$ થશે.View Solution
- 7આપાત કિરણ, પરાવર્તિત કિરણ અને બાહ્ય તરફ દોરેલ લંબ ને અનુક્રમે એકમ સદિશ $\overrightarrow{ a }, \overrightarrow{ b }$ અને $\overrightarrow{ c }$ દ્વારા દર્શાવામાં આવે છે. આ સદિશો વચ્ચેનો સાચો સંબંધ પસંદ કરો.View Solution
- 8ભૌતિકશાસ્ત્રની લેબોરેટરીમાં ટ્રાવેલીંગ માઈક્રોસ્કોપની મદદથી ગ્લાસના ચોસલાનો વક્રીભવનાંક માપવાના પ્રયોગમાં, વિદ્યાર્થી ગ્લાસના ચોસલાની સાયી જાડાઈ $5.25\,mm$ માપે છે અને જ્યારે ટ્રાવેલીગ માઈક્રોસ્કોપ મળતી (આભાસી) જાડાઈ $5.00\,mm$ છે. ટ્રાવેલીગ માઈક્રોસ્કોપમાં મુખ્ય, સ્કેલ ઉપર $1\,cm$ માં $20$ કાપાઓ અને $50$ વર્નિયર સ્કેલ પરના કાપાનું મૂલ્ય મુખ્ય સ્કેલ પરના $49$ કાપા બરાબર છે. ગ્લાસના ચોસલાનો વક્રીભવનાંક માપવામાં, મળતી ત્રુટિ $\frac{x}{10} \times 10^{-3}$ છે, તો $x=............$ થશે.View Solution
- 9એસ્ટ્રોનોમિકલ ટેલિસ્કોપની મોટવણી $8$ છે,ઓબ્જિેકિટવપીસ અને આઇપીસ વચ્ચેનું અંતર $54cm$ છે. તો આઇપીસ $f_e$ અને ઓબ્જિેકિટવપીસ $f_o$ ની કેન્દ્રલંબાઇ કેટલી હશે?View Solution
- 10જો એક લેન્સને વસ્તુ તરફ $40 \,cm$ થી $30\, cm$ અંતરે ખસેડવામાં આવે તો પ્રતિબિંબની મોટવણી સમાન રહે છે. (ગાણિતિક રીતે) લેન્સની કેન્દ્રલંબાઈ ......... $cm$ છે ?View Solution
