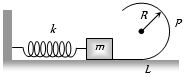
સ્પ્રિંગને બ્લોક દ્વારા કેટલી દબાવીને મૂકવાથી $P$ બિંદુ આગળ કેન્દ્રગામી બળ $mg$ મળે?
Diffcult
Download our app for free and get started
c
\(\frac{{mv_P^2}}{R} = mg\)
\(\frac{{mv_P^2}}{R} = mg\)
\(\therefore \,\,{v_P} = \sqrt {Rg} \)
\(v_p^2 = v_L^2 - 2gR\) (\({v^2} = {u^2} - 2gh)\)
\({v_L} = \sqrt {v_P^2 + 2gR} = \sqrt {Rg + 2gR} = \sqrt {3gR} \)
\(k = \frac{1}{2}\,mv_L^2\)\( = \frac{1}{2}\,m\, \times 3gR\)
\(\frac{1}{2}k{x^2} = \frac{1}{2}\,3m \times \,g\,R\)
\(\therefore x = \sqrt {\frac{{3m\,g\,R}}{k}} \).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક એન્જિન દ્વારા પાણી હોંસ પાઇપ મારફતે છોડવામાં આવે છે. હોસ પાઇપમાંથી બહાર નીકળતા પાણીનો વેગ $v$ અને હોસ પાઇપની એકમ લંબાઇ દીઠ બહાર આવતું દળ $m$ છે. પાણીને પૂરી પડાતી ગતિઊર્જાનો દર કેટલો હશે?View Solution
- 2$2 kg$ દળનો પદાર્થ $ 10 m/s $ વેગથી પૂર્વ દિશામાં અને સમાન દળ ધરાવતો પદાર્થ સમાન વેગથી દક્ષિણ દિશામાં ગતિ કરે છે.બંને અથડાતા બંને પદાર્થનો સંયુકત વેગ કેટલો થશે?View Solution
- 3View Solutionઘર્ષણરહિત સમક્ષિતિજ ટેબલ પર પડેલા એક નક્કર ચોસલા સાથે એક ગોળી અથડાય છે અને તેમાં ફસાય જાય છે તો શેનુ સંરક્ષણ થશે?
- 4View Solutionપદાર્થને ટાવર પરથી મુકત કરતાં પ્રથમ,બીજી અને ત્રીજી સેકન્ડમાં થયેલ કાર્યનો ગુણોત્તર કેટલો થાય ?
- 5એક $m$ દળવાળા સ્થિર પદાર્થને પ્રવેગ આપતાં તે $T$ સમયમાં $v$ જેટલો વેગ પ્રાપ્ત કરે છે. સમયના પદમાં પદાર્થને મળતો તત્કાલીન પાવર ........છે.View Solution
- 6$m $ દળનું એક વાહન સ્થિર સ્થિતિએથી પ્રવેગીત થાય છે. જો એન્જિન $p$ જેટલો અચળ પાવર અપાતુ હોય તો $ t $ સમયે વેગ કયા સૂત્રથી આપી શકાય?View Solution
- 7એક બોલ $ 'h' $ ઉંચાઈ પરથી મુક્ત રીતે પતન કરે છે. આ બોલ સતત પટકાઈને પાછો ફરે છે. તો $ 'n' $ વાર પાછો ફર્યા પછી બોલ વડે પ્રાપ્ત થતી ઉંચાઈ અને $n$ વાર પાછો ફરવા માટે બોલને લાગતો સમય શોધો.View Solution
- 8$3 kg$ દળનો એક પદાર્થ બળની અસર નીચે ગતિ કરતાં તે $S = \frac{{{t^3}}}{3}\;m$ સ્થાનાંતર કરે, તો બળ વડે પ્રથમ $2$ સેકન્ડમાં થતું કાર્ય કેટલા ................ ${J}$ હશે?View Solution
- 9જો વેગમાન $20\%$ વધારવામાં આવે તો ગતિઊર્જા $........\%$ જેટલી વધે છે.View Solution
- 10એક એન્જિન હોઝ માથી સતત પાણી ખેંચે છે. પાણી હોઝને વેગ $v$ અને નળીની એકમ લંબાઈ દીઠ દળ $m$ થી છોડે છે. જો આ નળી સપાટી પર અથડાય અને તત્કાળ સ્થિર સ્થિતિમાં આવે તો આ સપાટી પર લાગતું બળ કેટલું હશે?View Solution