સ્થાનાંતર પદ્ધતિમાં, બહિર્ગોળ લેન્સ તેના બે અલગ સ્થાન માટે વસ્તુનું વાસ્તવિક પ્રતિબિંબ રચે છે. જો બંને કિસ્સામાં પ્રતિબિબની ઊંચાઈ $24 \,cm$ અને $6\, cm$ હોય, તો વસ્તુની ઊંચાઈ ........ $cm$ છે ?
Easy
Download our app for free and get started
d
(d)
(d)
In displacement method
\(m_1 m_2=1\)
\(\frac{h_1}{h} \times \frac{h_2}{h}=1\)
\(h=\sqrt{h_1 h_2}\)
\(h=\sqrt{24 \times 6}\)
\(h=12 \,cm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમતલીય બહિર્ગોળ લેન્સનો વક્રીભવનાંક $1.5$ અને વક્રતા ત્રિજ્યા $30\,cm $ છે. તેની વક્ર સપાટી પર સિલ્વર લગાડવામાં આવે છે. હવે આ લેન્સનો ઉપયોગ કોઈ વસ્તુનું પ્રતિબિંબ રચવા થાય છે. આ લેન્સથી ક્યા......$cm$ અંતરે વસ્તુને મૂકતાં તેટલા જ આકારનું વાસ્તવિક પ્રતિબિંબ મળશે?View Solution
- 2બે સમતલ અરીસા એકબીજાથી $45^o$ ના ખૂણે છે. જો પદાર્થને તેમની વચ્ચે મૂકવામાં આવે તો કેટલા પ્રતિબિંબ રચાશે?View Solution
- 3એક વસ્તુ અંતર્ગોળ અરીસાની અક્ષ પર મુખ્ય કેન્દ્રથી દૂર જાય છે.તો તેના માટે રેખીય મોટવણી $(m)$ વિરુદ્ધ અરીસાથી વસ્તુ અંતર $(x)$ નો આલેખ કેવો મળે?View Solution
- 4View Solutionશ્રી.સી.વી.રામન ને પ્રકાશની કઇ ધટના માટે નોબલ આપવામાં આવ્યું હતું?
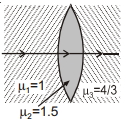
- 5બંને બાજુ બહિર્ગોળ સપાટીની વક્રતા ત્રિજ્યા $20 \,cm$ છે, તો આપેલ ગોઠવણીમાં હવામાં મૂકેલી વસ્તુ માટે કેન્દ્રની કેન્દ્રલંબાઈ .......... $cm$View Solution
- 6$10\,\,cm$ કેન્દ્રલંબાઈ ધરાવતાં અપસારી લેન્સથી એક બિંદુવત ઉદ્દગમને $15\,\,cm$ ના અંતરે મૂકેલો છે. $12\,\, cm$ કેન્દ્રલંબાઈનાં અંત:ર્ગોળ અરીસાને .......$cm$ મૂકેલ હોવો જોઈએ કે જેથી તેની જાતે વસ્તુ પર વાસ્તવિક પ્રતિબિંબ રચાયેલું હોય?View Solution
- 7$30\, cm$ કેન્દ્રલંબાઇવાળો બર્હિગોળ લેન્સ અને $10\, cm$ કેન્દ્રલંબાઇવાળો અંર્તગોળ લેન્સ એકબીજાથી $d$ અંતરે સમઅક્ષીય રીતે મૂકેલા છે.સમાંતર કિરણો બર્હિગોળ લેન્સ પર પાડવામાં આવે છે. ત્યારે અંર્તગોળ લેન્સમાંથી નીકળતા કિરણો પણ સમાંતર છે.તો $d=$______$cm$View Solution
- 8અંતર્ગોળ અરીસાના કેન્દ્રલંબાઈ $50\, cm $ છે. પદાર્થને .......$cm$ જગ્યાએ મૂકતાં પ્રતિબિંબ બમણા આકારનું વાસ્તવિક અને વ્યસ્ત મળશે.View Solution
- 9એક વસ્તુને સમતલ અરીસાની સામે $12\,cm$ અંતરે મૂકેલ છે. અરીસા વડે આભાસી અને ચત્તુ પ્રતિબિંબ રચાય છે. હવે અરીસાને સ્થિર વસ્તુ તરફ $4\,cm$ ખસેડવામાં આવે છે. પ્રતિબિંબનું સ્થાન .......... જેટલું ખસશે.View Solution
- 10${f_1}$ અને ${f_2}$ કેન્દ્રલંબાઇ ધરાવતા લેન્સ સંપર્કમાં હોય,ત્યારે પ્રતિબિંબ $60cm$ અંતરે મળે છે.જયારે બંને લેન્સને $10cm $ અંતરે રાખતા પ્રતિબિંબ $30cm$ અંતરે મળે છે.તો ${f_1}$ અને ${f_2}$ કેટલા થાય?View Solution