બોમ્બ ના ત્રણ સરખા ટુકડા થાય છે
\(\therefore \,\,\,{{\text{m}}_{\text{1}}}\,\, = \,\,{m_2}\,\, = \,\,{m_3}\,\, = \,\,m\)
હવે, \({{\text{m}}_{\text{1}}}\) ટુકડા નો વેગ \(\mathop {{{\text{v}}_{\text{1}}}}\limits^ \to \,\, = \,\,9\,\,\hat i\,\,m/s,\,\,{{\text{m}}_{\text{2}}}\,\)
ટુકડા નો વેગ \(\,\mathop {{{\text{v}}_{\text{2}}}}\limits^ \to \,\, = \,\,12\,\,\hat j\,\,\,m/s,\,\,{{\text{m}}_{\text{3}}}\) ટુકડા નો વેગ \(\mathop {{{\text{v}}_{\text{3}}}}\limits^ \to \,\, = \,\,?\)
વેગમાં સંરક્ષણ ના નિયમ મુજબ \(\,{\text{M}}\,\,\mathop {\text{v}}\limits^ \to \,\, = \,\,{{\text{m}}_{\text{1}}}\,\mathop {{v_1}}\limits^ \to \,\, + \,\,\,{m_2}\,\mathop {{v_2}}\limits^ \to \,\, + \,\,{m_3}\,\mathop {{v_3}}\limits^ \to \)
\(0\,\, = \,\,m\,(9\,\,\hat i)\,\, + \,\,m\,\,(12\,\,\hat j)\,\, + \,\,m\,\,\mathop {{v_3}}\limits^ \to \,\,\)
(બોમ્બ પ્રારંભ માં સ્થિર છે)
\(\therefore \,\,\mathop {{{\text{v}}_{\text{3}}}}\limits^ \to \,\, = \,\, - \,\,9\,\,\hat i\,\, - \,\,12\,\,\hat j\,\,\,\,\,\,\,\therefore \,\,\left| {\mathop {{v_3}}\limits^ \to } \right|\,\, = \,\,\,\sqrt {{{( - 9)}^2}\, + \,\,{{( - 12)}^2}} \,\,\)
\( = \,\,\sqrt {81\,\, + \,\,144} \,\,\,\,\therefore \,\,\,\,\left| {\mathop {{v_3}}\limits^ \to } \right|\,\, = \,\,15\,\,m\,\,{s^{ - 1}}\)
Download our appand get started for free
Similar Questions
- 1$m_1$ દળ અને $v_1 \hat i$ વેગ ધરાવતો પદાર્થ $m_2$ દળ અને $v_2 \hat i$ વેગ ધરાવતા પદાર્થ સાથે રેખીય અથડામણ અનુભવે છે. અથડામણ પછી $m_1$ અને $m_2$ દળ અનુક્રમે $v_3 \hat i$ અને $v_4 \hat i$ વેગથી ગતિ કરે છે. જો $m_2 = 0.5\, m_1$ અને $v_3 = 0.5\, v_1$ હોય તો $v_1$ કેટલો થાય?View Solution
- 2એક લિફ્ટ $a$ જેટલા પ્રવેગથી નીચે આવી રહી છે.લિફ્ટમાં ઊભેલી વ્યકિત એક બોલ પડતો મૂકે છે,તો લિફ્ટમાં ઊભેલી વ્યકિત અને બહાર જમીન પર ઊભલી વ્યકિત તે આ બોલના પ્રવેગ અનુક્રમે _______ અને ________ માપશેView Solution
- 3$100g$ ન પદાર્થને $20\, m \,sec^{-1}$ વેગથી સમક્ષિતીજ સાથે $30^°$ ના ખૂણે પ્રક્ષિપ્ત કરતા મહતમ ઊચાઇએ તેના વેગમાનમા કેટલા...........$kg\,m\,{\sec ^{ - 1}}$ ફેરફાર થાય?View Solution
- 4$5\, kg$ નો પદાર્થ ઉદ્ગમ બિંદુથી શરૂઆતના $\overrightarrow {u\,} \, = \,30\hat i + 40\hat j\,m{s^{ - 1}}$ વેગથી ગતિ કરે છે.જો તેના પર બળ $\overrightarrow {F\,} = - (\hat i + 5\hat j)N$ લાગે,તો વેગનો $Y-$ ઘટક શૂન્ય થતાં ........ $\sec$ લાગે.View Solution
- 5$1000\;kg$ ના રોકેટમાં બળતણના વપરાશનો દર $ 40 kg/s$ છે. રોકેટમાંથી બહાર આવતાં વાયુનો વેગ $5 \times {10^4}m/s$ છે. તો રોકેટ પર કેટલું બળ લાગતું હશે?View Solution
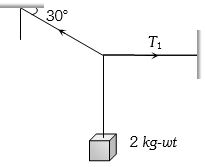
- 6આપેલ તંત્ર માટે સમક્ષિતિજ દોરીમાં તણાવ $T_1 \,\,kg-wt$ માં કેટલો થાય?View Solution
- 7$3\, kg$ અને $4\, kg$ દળ ના બે પદાર્થો ને ઘર્ષણરહિત ગરગડી પરથી પસાર થતી દળરહિત દોરી સાથે લટકાવેલા છે. તો તંત્રનો પ્રવેગ ........ $m/{s^2}$ થશે. $(g = 9.8\,m/{s^2})$View Solution
- 8View Solutionએક બોમ્બ હવામાં ગતિ કરતાં કરતાં ચાર અસમાન ટુકડાઓમાં વિસ્ફોટ પામે છે. નીચેનામાંથી શેનું સંરક્ષણ થતું હશે?
- 9એક $3 kg$ દળનો એક બોલ $10 m/sec$ ના વેગથી $60^o$ ના ખૂણે દિવાલ પર અથડાય છે અને અથડામણ પછી તે તેટલા જ ખૂણે અને તેટલી જ ઝડપે પાછો ફરે છે. $MKS$ એકમમાં બોલના વેગમાનનો ફેરફાર કેટલો હશે?View Solution
- 10આ પ્રશ્નમાં વિધાન $1$ અને વિધાન $2$ છે. તો આપેલા ચાર વિકલ્પો માથી બંને વિધાનો માટે સાચો વિકલ્પ પસંદ કરો.View Solution
વિધાન $1$: ઘોડાગાડી ને તમે ધક્કો મારો તો તે ચાલતી નથી પરંતુ તે સમાન મૂલ્ય અને વિરુદ્ધ દિશામાં બળ લગાવીને તમને ધકેલે છે.
વિધાન $2$: વિધાન $1$ માં જણાવેલા બળો એકબીજા ની અસરને નાબૂદ કરે છે તેથી ઘોડાગાડી ચાલતી નથી
