સ્ટીલ પર જ્યારે $3 .5 \times 10^8\,\,N\,m^{-2}$ જેટલુ આકાર પ્રતિબળ લગાવવામાં આવે ત્યારે તે તૂટે છે.તો $0.3\,cm$ જાડાઈના સ્ટીલના પતરામાં $1\,cm$ વ્યાસ વાળો હૉલ કરવા માટે કેટલા બળની જરૂર પડે?
JEE MAIN 2014, Diffcult
c
Shearing strain is created along the side surface of the punched disk. Note that the forces exerted on the disk are exerted along
Shearing strain is created along the side surface of the punched disk. Note that the forces exerted on the disk are exerted along
the circum ference of the disk, and the total force exerted on its center only.
Letus assume that the shearing stress along the side surface of the disk is uniform, then
\(F > \int\limits_{Surface} {d{F_{\max }} = \int\limits_{surface} {{\sigma _{\max }}dA = {\sigma _{\max }}} \int\limits_{surface} {dA} } \)
\( = \int {{\sigma _{\max }}} .A = {\sigma _{\max }}.2\pi \left( {\frac{D}{2}} \right)h\)
\( = 3.5 \times {10^8} \times \left( {\frac{1}{2} \times {{10}^{ - 2}}} \right) \times 0.3 \times {10^{ - 2}} \times 2\pi \)
\( = 3.297 \times {10^4} = 3.3 \times {10^4}N\)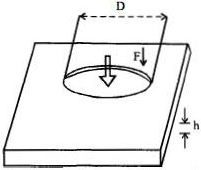
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$Y = 2.0 \times {10^{11}}\,N/{m^2}$ યંગ મોડયુલસ ધરાવતા અને $1m$ લંબાઇ ધરાવતા તારને બે દ્રઢ આધાર વચ્ચે બાંધેલ છે.તેનું તાપમાન ${100^o}C$ વધારતાં તેમાં કેટલી ઊર્જાનો સંગ્રહ થાય? ($\alpha = 18 \times {10^{ - 6}}{\,^o}{C^{ - 1}}$,$A = 1\,c{m^2}$)View Solution
- 2એક લોખંડના સળિયાની ત્રિજ્યા $20\,mm$ અને લંબાઈ $2.0\,m$ છે.$62.8\,kN$ નું બળ તેમની લંબાઈને સાપેક્ષે ખેંચે છે. લોખંડનો યંગ અચળાંક $2.0 \times 10^{11}\,N / m ^2$ છે. તારમાં ઉત્પન્ન થતી પ્રતાન વિકૃતિ ........ $\times 10^{-5}$ છે.View Solution
- 3View Solutionઆકૃતિ પ્રતિબળ - વિકૃતિનો આલેખ દર્શાવે છે જે બે જુદા જુદા તાપમાને છે તો.
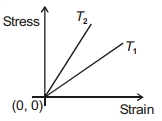
- 4ચોક્કસ દબાણ $P$ ને $1$ લીટર પાણી અને $2$ લીટર પ્રવાહી પર અલગથી લાગુ પાડવામાં આવે છે. પાણી સંકોચાઈને $0.01 \%$ થાય છે, જ્યારે પ્રવાહી સંકોચાઈને $0.03 \%$ થાય છે. પાણીનો અને પ્રવાહીનો બલ્ક મોડ્યુલસ ગુણોત્તર $\frac{3}{x}$ છે. $x$ ની કિંમત કેટલી હશે?View Solution
- 5View Solutionતારનો બળ અચળાંક કોના પર આધાર રાખે નહીં ?
- 6$0.3\; \mathrm{m}$ લંબાઈના તારના એક છેડે $\mathrm{m}=10\; \mathrm{kg}$ નો પદાર્થ બાંધેલો છે.તેને અવકાશમાં મહત્તમ કેટલી કોણીય ઝડપથી($rad \;s^{-1}$ માં) ફેરવી શકાય?(તારનું મહત્તમ બ્રેકિંગ પ્રતિબળ $=4.8 \times 10^{7} \;\mathrm{Nm}^{-2}$ અને તારના આડછેડનું ક્ષેત્રફળ $=10^{-2}\; \mathrm{cm}^{2}$ છે)View Solution
- 7સમતાપી $E_\theta$ અને સમોષ્મી $E_\phi$ બલ્ક મોડયુલસ વચ્ચેનો સંબંધ નીચે પૈકી કયો છે? $(\gamma = {C_p}/{C_v})$View Solution
- 8એક ધાતુ માટે આંતરઆણ્વિય અંતર $3 \times {10^{ - 10}}\,m$ છે.જો આંતરિક અણું માટે બળ અચળાંક $3.6 \times {10^{ - 9}}\,N/{{\buildrel _{\circ} \over {\mathrm{A}}} }$,હોય તો યંગ મોડ્યુલસનું મૂલ્ય $N/{m^2}$ માં કેટલું થાય?View Solution
- 9$40^{\circ}\,C$ તાપમાને રહેલા $L$ લંબાઈના સ્ટીલના વાયરને છત સાથે લટકાવેલ છે અને બીજા છેડા પર $m$ દળ લટકાવેલ છે. તેની મૂળ લંબાઈ $L$ પાછી મેળવવા માટે તને $40^{\circ}$ થી $30^{\circ}$ સુધી ઠંડો કરવામાં આવે છે. વાયરની ત્રિજ્યા $1\,mm$, રેખીય ઉષ્મા પ્રસણાંક $10^{-5} /{ }^{\circ}\,C$ અને સ્ટીલનો યંગ મોડ્યુલસ $10^{11}\,N /$ $m ^2$ છે. ધારી લો કે $L \gg $ વ્યાસ છે. $m$ નું મૂલ્ય $kg$ માં ?View Solution
- 10જો તાર પર $Mg$ દળ લગાવતા તેની લંબાઈમાં $l$ વધારો થાય તેના પર થયેલું કુલ કાર્ય કેટલું હશે $?$View Solution
