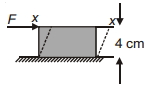
સ્ટીલના પ્લેટનું ક્ષેત્રફળ $1 \,cm ^2$ અને જાડાઈ $4 \,cm$ દેઢ ટેકા સાથે રાખેલ છે. જ્યારે સ્પર્શીયય બળ $10 \,kN$ જેટલુ ભાગે છે ત્યારે આકૃતિમાં દર્શાવ્યા પ્રમાણે ફેરફાર થાય છે. તેમાં થતુ $x$ જેટલુ ઉપરના તરફનુ અંતરનો ફેરફાર .............. $m$ (Modulus of rigidity for steel is $8 \times 10^{11} \,N / m ^2$ )

Medium
b
(b)
(b)
\(\text { Modulus of rigidity }(G)=\frac{\text { Force } \times \text { Length }}{\text { Area } \times \text { Lateral displacement }}=\frac{F L}{A \times \Delta x}\)
\(F=10 \,kN =10 \times 10^3 \,N\)
\(L=4 \,cm =0.04 \,m\)
\(A=1 \,cm ^2=1 \times 10^{-4} \,m ^2\)
\(G=8 \times 10^{11}\,N / m ^2\)
Substituting values
\(8 \times 10^{11}=\frac{10 \times 10^3 \times 0.04}{1 \times 10^{-4} \times \Delta x}\)
\(\Delta x=\frac{10 \times 10^3 \times 0.04}{1 \times 10^{-4} \times 8 \times 10^{11}}=5 \times 10^{-6} \,m\)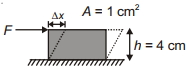
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સ્ટીલ પર જ્યારે $3 .5 \times 10^8\,\,N\,m^{-2}$ જેટલુ આકાર પ્રતિબળ લગાવવામાં આવે ત્યારે તે તૂટે છે.તો $0.3\,cm$ જાડાઈના સ્ટીલના પતરામાં $1\,cm$ વ્યાસ વાળો હૉલ કરવા માટે કેટલા બળની જરૂર પડે?View Solution
- 2View Solutionસ્થિતિસ્થાપકતાની મહત્તમ અસર કોના માં જોવા મળે ?
- 3૨બરના એક બોલને દરિયાની સપાટીથી કેટલી ઊંડાઈ(mમા)એ લઈ જતા તેના કદમાં $0.02 \%$ નો ઘટાડો થાય?(દરિયાના પાણીની ઘનતા $=10^3 \mathrm{kgm}^{-3}$, રબરનો બલ્કમોડ્યુલસ $=9 \times 10^8 \mathrm{Nm}^{-2}$, and $\mathrm{g}=$$10 \mathrm{~ms}^{-2}$ લેવું.)View Solution
- 4$0.1 \,m$ બાજુવાળા સમઘન બ્લોકની ઉપરની બાજુ પર $100 \,N$ નું સ્પર્શીય બળ લગાડતાં તે નીચેની બાજુની સાપેક્ષે $0.02 \,cm$ ખસે છે,તો સ્પર્શીય વિકૃતિ કેટલી થાય?View Solution
- 5એક સમાન ધાત્વીય તાર પર $F$ જેટલું રેખીય બળ લગાડવામાં આવે ત્યારે તેની લંબાઈ $0.04 \,m$ જેટલી વધે છે. જો તેની લંબાઈ અને વ્યાસ બમણો કરવામાં આવે તો તે સમાન બળ માટે પ્રતાન (લંબાઈ) માં વધારો ........ $cm$ થશે.View Solution
- 6જ્યારે તાણ $T _{1}$ હોય ત્યારે ધાત્વિક તારની લંબાઈ $\ell_{1}$ છે. જ્યારે તાણ $T _{2}$ હોય ત્યારે તે $\ell_{2}$ હોય છે. તારની મૂળ લંબાઈ ........ હશે.View Solution
- 7$Y =7.0 \times 10^{10}\,N / m ^2$ યંગ મોડ્યુલસ ધરાવતો એક એલ્યુમિનિયમનો સળિયો $0.04 \%$ સ્થિતિ સ્થાપક તણાવ (વિકૃતિ) અનુભવે છે. $J/m^3$ માં સંગ્રહાતી ઊર્જા પ્રતિ એકમ ધનફળ છે.View Solution
- 8View Solutionતાર પરનું તણાવ અચાનક દૂર કરવામાં આવે તો ..
- 9તારનો એક છેડો છત સાથે જડિત છે અને બીજા છેડાથી $2 \mathrm{~kg}$ નું દળ લટકાવેલ છે. આવો સમાન બીજો તાર ભારના છેડે થી લટકાવવામાં આવે છે અને નીચેના તારને છેડે $1 \mathrm{~kg}$ નું દળ લટકાવવામાં આવે છે. તો ઉપરના તારમાં અને નીચેના તારમાં પ્રવર્તતી સંગતવિકૃતિતોનો ગુણોત્તર_____________હશે.View Solution
[તારનો આડઇેદનું ક્ષેત્રણ $=0.005 \mathrm{~cm}^2 \gamma=2 \times 10^{11} \mathrm{Nm}^{-2}$ અને $\mathrm{g}=10 \mathrm{~ms}^{-2}$ ]
- 10$2\,c{m^2}$ આડછેદ ધરાવતા રબરની લંબાઇ બમણી કરવા માટે જરૂરી બળ $2 \times {10^5}$ dynes છે,તો યંગ મોડયુલસ $dyne/c{m^2}$ માં કેટલો થાય ?View Solution
