સ્ટોક્સના નિયમની સકાચણી કરવા માટે કરેલા પ્રયોગમાં $r$ ત્રિજ્યા અને $\rho$ ઘનતા ધરાવતા એક ગોળ દડાને પાણી ભરેલા પાત્રમાં પાણીની સપાટીથી $h$ ઊંચાઈ પરથી મુક્ત કરવામાં આવે છે. જો પાણીની અંદર દડાનો ટર્મિનલ વેગ એ પાણીની અંદર આવતા પહેલા દડાના વેગ જેટલો હોય તો ઊંચાઈ $h$ કોના સમપ્રમાણમાં હશે? (હવાનો શ્યાનતાગુણાંક અવગણો)
JEE MAIN 2020, Medium
Download our app for free and get started
b
After falling through h, the velocity be equal to terminal velocity
After falling through h, the velocity be equal to terminal velocity
\(\sqrt{2 gh }=\frac{2}{9} \frac{ r ^{2} g }{\eta}\left(\rho_{\ell}-\rho\right)\)
\(\Rightarrow h =\frac{2}{81} \frac{ r ^{4} g \left(\rho_{\ell}-\rho\right)^{2}}{\eta^{2}}\)
\(\Rightarrow h \propto r ^{4}\)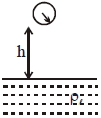
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$0.1 \,m ^2$ ક્ષેત્રફળ ધરાવતી સમતલ પ્લેટને સમતલ સપાટી પર મૂકેલી છે અને તે $10^{-5 }\,m$ જાડાઈની તેલની ફિલ્મ વડે સપાટીથી અલગ કરેલી છે. જેની શ્યાનતા પ્લેટને $1.5 \,N sm ^{-2}$ છે. $1 \,mm s ^{-1}$ અચળ ઝડપથી સપાટી પર ગતિ કરાવવા માટે જરરી બળ ........ $N$ હશે.View Solution
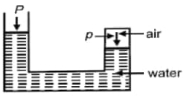
- 2મર્યાદિત હવાનું દબાણ $p$ છે. જો વાતાવરણનું દબાણ $P$ છે તો...View Solution
- 3કોઇ લાંબા નળાકારીય પાત્રમાં પ્રવાહી અડધે સુધી ભરેલ છે. જ્યારે પાત્ર પોતાની ઉર્ધ્વ અક્ષને અનુલક્ષીને પરિભ્રમણ કરે છે ત્યારે દિવાલની નજીક (અડીને) પ્રવાહી ઊપર ચઢે છે. જો પાત્રની ત્રિજ્યા $5 \,cm$ અને તેની ચાક ઝડપ $ 2$ ભ્રમણ પ્રતિ સેકન્ડ હોય તો તેના કેન્દ્ર (મધ્યભાગ) અને છેડાની વચ્ચે ઊંચાઈનો તફાવત, $cm$ માં કેટલો હશે?View Solution
- 4તળાવના તળિયેથી પરપોટો સપાટી પર આવતા ત્રિજયા બમણી થાય છે. $H$ ઊંચાઇના પાણીના સ્તંભનું દબાણ વાતાવરણ જેટલું હોય,તો તળાવની ઊંડાઇ કેટલી થાય? ( પ્રક્રિયા સમતાપી ધારો )View Solution
- 5View Solutionએક બરફનો બ્લોક એ એવા પ્રવાહીમાં તરે છે જેની ઘનતા પાણી કરતા ઓછી છે. બ્લોકનો અમુક ભાગ પ્રવાહીની બહાર રહે છે, જ્યારે તે પુરેપુરો પીગળી જાય, તો પ્રવાહીનું લેવલ
- 6ગોળાકાર વરસાદના ટીપાંનો અંતિમ (ટર્મીનલ) વેગ ($v_t$) ધણાં બધા પ્રાચલો ઉપર આધાર રાખે છે. પરંતુ $\left(v_{t}\right)$ નો ગોળાકાર વરસાદના ટીપાંની ત્રિજ્યા $(r)$ સાથેનો ફેરફાર......... પર આધાર રાખે છે.View Solution
- 7ઉપરના વાતાવરણમાં $0.01 \mathrm{~mm}$ ત્રીજ્યાના પાણીના સૃક્ષ્મ ટીપાઓ રચાય છે અને $10 \mathrm{~cm} / \mathrm{s}$ અંતિમ વેગથી પડે છે. ધાનિકરણ દ્વારા જો આવા $8$ ટીપાઓ ભેગા મળીને એક મોટુ ટીપું રચે, તો નવો અંતિક વેગ. . . . . . $\mathrm{cm} / \mathrm{s}^{-1}$ થશે.View Solution
- 8જમીન પર રાખેલ ટાંકીમાં $10\,m$ ઊંચાઈ સુધી પાણી ભરેલ છે.તેમાં બે જમીનથી $3\, m$ અને $7\, m$ ઊંચાઈ કાણાં પડેલા છે.તો બહાર આવતા પાણી માટે શું કહી શકાય?View Solution
- 9બે કોપરના પાત્ર $A$ અને $B$ સમાન પાયાનું ક્ષેત્રફળ પરંતુ અલગ આકાર ધરાવે છે. એક ચોક્કસ સામાન્ય ઊંચાઈ સુધી પાણી ભરતા $A$ દ્વારા રોકતું કદ $B$ કરતાં બમણું મળે છે. તો નીચેનામાંથી સાચું વિધાન કયું છે?View Solution
- 10જો $p$ એ ધનતા અને $\eta$ એ પ્રવાહીની શ્યાન્તા હોય કે જે $d$ વ્યાસ ધરાવતી નળીમાંથી વહે છે. રેનોલ્ડ નંબર $R_{ e }$ નું સાચું સૂત્ર ........... હશે.View Solution