ઉપરના વાતાવરણમાં $0.01 \mathrm{~mm}$ ત્રીજ્યાના પાણીના સૃક્ષ્મ ટીપાઓ રચાય છે અને $10 \mathrm{~cm} / \mathrm{s}$ અંતિમ વેગથી પડે છે. ધાનિકરણ દ્વારા જો આવા $8$ ટીપાઓ ભેગા મળીને એક મોટુ ટીપું રચે, તો નવો અંતિક વેગ. . . . . . $\mathrm{cm} / \mathrm{s}^{-1}$ થશે.
JEE MAIN 2024, Diffcult
b
\(\mathrm{m}=\text { mass of small drop }\)
\(\mathrm{m}=\text { mass of small drop }\)
\(\mathrm{M}=\text { mass of bigger drop }\)
\(\mathrm{V}_{\mathrm{t}}=\frac{2}{9} \frac{\mathrm{R}^2(\rho-\sigma) \mathrm{g}}{\eta}\)
\(8 \propto \mathrm{m}=\mathrm{M}\)
\(8 \mathrm{r}^3=\mathrm{R}^3 \Rightarrow \mathrm{R}=2 \mathrm{R}\)
\(\text { as } \mathrm{V}_{\mathrm{t}} \times \mathrm{R}^2 \because \text { Radius double so } \mathrm{V}_{\mathrm{t}} \text { becomes } 4 \text { time }\)
\(\therefore 4 \times 10=40 \mathrm{~cm} / \mathrm{s}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
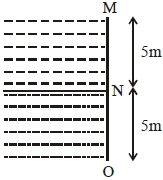
- 1આકૃતિમાં દર્શાવ્યા મુજબ $10\; \mathrm{m}$ ના ચોરસ પાત્રમાં બે પ્રવાહી ભરેલા છે જેમની ઘનતા $\rho_{1}$ અને $\rho_{2}\left(\rho_{2}=2 \rho_{1}\right)$ છે.બંને પ્રવાહીની ઊંચાઈ $5 \;\mathrm{m} .$ છે.આ પ્રવાહીના કારણે $MN$ અને $NO$ પર લાગતા બળનો ગુણોત્તર કેટલો મળે?View Solution
(પ્રવાહી એકબીજામાં મિશ્ર થતાં નથી)
- 2$1\,mm$ ત્રિજ્યા અને $10.5\,g / cc$ ની ધનતા ધરાવતી ગોળીને $9.8$ પોઈઝ શ્યાનતા ગુણાંક અને $1.5\,g / cc$ ધનતા ધરાવતા ગ્લિસરીનમાં પડવા દેવામા આવે છે. જયારે ગોળી અચળ વેગ પ્રાપ્ત કરે ત્યારે શ્યાનતાનું બળ $3696 \times 10^{-x}\,N$ છે.તો $x$ નું મૂલ્ય કેટલું હશે ?View Solution
$( g =9.8\,m / s ^2$ આપેલું છે.)
- 3$5\, cm$ ત્રિજ્યા ધરાવતી પાઇપમાથી પાણી $100\,$ લિટર પ્રતિ મિનિટ ના દરથી આવે તો પ્રવાહનો રેનોલ્ડ નંબર કયા ક્રમનો હશે? (પાણીની ઘનતા $= 1000\, kg/m^3$, પાણીનો શ્યાનતાગુણાંક $= 1\, mPa\, s$)View Solution
- 4$w$ જાડાઈ ધરાવતા અને $H$ ઊંંચાઈ ધરાવતા ડેમમાં પાણી ભરવામાં આવે છે, તો ડેમ પર લાગુ પડતું પરીણામી બળ.View Solution
- 5આકૃતિમાં દર્શાવ્યા મુજબ ના વ્યાસ ધરાવતી બે ભુજાએમાં પાણી ભરેલું હોય તેવો હાઈડ્રોલીક પ્રેસને દર્શાવેલ છે. તેના પાતળી ભુજામાં રહેલ પાણી ઉપર $10 \mathrm{~N}$ નું બળ લગાડવામાં આવે છે. પાણીને સંતુલન સ્થિતિમાં રાખવા માટે જાડી (મોટી) ભુજામાં રહેલ પાણી ઉપર લગાવવું પડતું બળ. . . . . . $\mathrm{N}$ હશે.View Solution

- 6લોહી ચઢાવવાની એક પ્રક્રિયામાં સોય $2000\, Pa$ ગેજ દબાણ હોય તેવી શિરામાં દાખલ કરેલ છે. લોહીભરેલું પાત્ર કેટલી ઊંચાઈએ મૂકવું જોઈએ કે જેથી લોહી શિરામાં દાખલ થવાની શરૂઆત થાય ? (સંપૂર્ણ લોહીની ઘનતા $\rho=1.06 \times 10^{3} \;kg m ^{-3}$)View Solution
- 7$0.5\,m$ લંબાઈ ધરાવતો ઘન પાણી પર તરે છે જેનું $30\%$ કદ પાણીની અંદર છે. બ્લોક પર મહત્તમ ......$kg$ વજન મૂકી શકાય કે જેથી તે સંપૂર્ણ પાણીમાં ડૂબી ના જાય. [પાણીની ઘનતા $= 10^3\,kg/m^3$ ]View Solution
- 8બે જુદાં જુદાં પ્રવાહી સમાન ત્રિજયાની નળીમાં વહે છે,તેમનાં શ્યાનતા ગુણાંકનો ગુણોત્તર $52:49 $ અને ઘનતાનો ગુણોત્તર $13:1$ હોય,તો ક્રાંતિવેગનો ગુણોત્તર કેટલો થાય?View Solution
- 9View Solutionસ્પ્રે કોના નિયમ પર આધાર રાખે છે.
- 10એકબીજામાં મિશ્રણ ન થઈ શકતા હોય, તેવા પ્રવાહીઓ કે જેમની ઘનતા $\rho$ અને $n\rho ( n>1) $ છે, જે કોઇ પાણીમાં ભરેલાં છે.દરેક પ્રવાહીની ઊંચાઇ $h$ છે. $L$ લંબાઇ અને $ d$ ઘનતાના એક નળાકારને આ પાત્રમાં રાખવામાં આવે,ત્યારે આ નળાકાર આ પાત્રમાં એવી રીતે તરે છે, કે જેથી તેની અક્ષ શિરોલંબ રહે તથા પ્રવાહીમાં તેની લંબાઇ $PL(P < 1)$ રહે છે, તો ઘનતા $d$ કેટલી હશે?View Solution
