સુસંબદ્ધ ઉદગમમાથી $\lambda $ તરંગલંબાઇનો પ્રકાશ આવે જે $b$ પહોળાઈની સ્લીટને પ્રકાશિત કરે છે.જો સ્લીટથી $1\;m$ અંતરે રહેલા પડદા પર મળતી વિવર્તનની ભાતમાં બીજુ અને ચૌથુ ન્યૂનતમ મધ્યમાન મહત્તમથી $3\, cm$ અને $6\, cm$ એ મળે છે, તો મધ્યમાન મહત્તમની પહોળાઈ($cm$ માં) કેટલી હશે?
JEE MAIN 2017, Diffcult
b
For secondary minima,
For secondary minima,
\(b \sin \theta=n \lambda \Rightarrow \sin \theta=\frac{n \lambda}{b}\)
Distance of \(\mathrm{n}^{\text {th }}\) secondary minima \(\mathrm{x}=\mathrm{D} \sin\, \theta\)
or \(\sin \theta_{1}=\frac{x_{1}}{D}\)
\(\sin \theta_{1}=\frac{2 \lambda}{b}\)
\(n=4\)
\(\sin \theta_{2}=\frac{4 \lambda}{b}=\frac{x_{2}}{D}\)
\(x_{2}-x_{1}=\frac{4 \lambda}{b}-\frac{2 \lambda}{b}=\frac{2 \lambda}{b}\)
\(3=\frac{2 \lambda}{b} \Rightarrow b=\frac{2 \lambda}{3}\) ...... \((i)\)
Width of central maxima \(=\frac{2 \lambda}{b}\)
\(=\frac{2 \lambda}{\frac{2 \lambda}{3}}=3 \mathrm{cm}\) ... from eq. \((i)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક સ્લિટ વડે થતા ફ્રોનહોફર વિવર્તનના કિસ્સામાં મધ્યસ્થ અધિકતમની તીવ્રતા $I_0$ છે. જો સ્લિટની પહોળાઈ બમણી કરવામાં આવે, તો તેની તીવ્રતા કેટલી હશે ?View Solution
- 2યંગના ડબલ સ્લિટ પ્રયોગમાં બંને સ્લિટ સુસંબદ્વ ઉદગમ તરીકે વર્તે છે. બંને સ્લિટમાંથી નીકળતા તરંગનો કંંપવિસ્તાર $A$ અને તરંગલંબાઈ $\lambda$ છે. બીજા એક પ્રયોગમાં બંને સ્લિટ અસુસંબદ્વ ઉદગમ તરીકે વર્તે છે. (કંંપવિસ્તાર અને તરંગલંબાઈ સમાન છે.) પડદાના મધ્ય બિંદુ આગળ તીવ્રતાનો ગુણોત્તર કેટલો થાય?View Solution
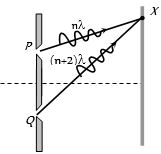
- 3યંગના ડબલ સ્લિટના પ્રયોગમાં $PX $ અને $QX$ પથની લંબાઇ $ n\lambda $ અને $ (n + 2)\lambda $ છે,મધ્ય શલાકાની તીવ્રતા શૂન્ય હોય,તો $X $ આગળ...View Solution
- 4સ્લિટની પહોળાઇ $ 0.2 mm$ અને પ્રકાશની તરંગલંબાઇ $ 500nm $ છે,સ્લિટથી પડદા વચ્ચેનું અંતર $80cm $ છે,તો મધ્યસ્થ અધિકતમની પહોળાઇ કેટલા ......$mm$ થાય?View Solution
- 5યંગના બે સ્લિટના પ્રયોગમાં, મધ્યસ્થ મહતમથી $5$મી પ્રકાશિત શલાકાનું સ્થાન $5\,cm$ આગળ મળે છે. સ્લિટ અને પડદા વચ્ચેનું અંતર $1\,m$ અને વપરાયેલ એકરંગી પ્રકાશની તરંગલંબાઈ $600\,nm$ છે. સ્લિટો વચ્યેનું અંતર $............\mu m$ છે.View Solution
- 6વક્રીભવનાંક ($n = 1.5)$ ધરાવતા કાંચ પર ધ્રુવીભવન કોણે અધ્રુવીભૂત પ્રકાશ આપાત કરતાં...View Solution
- 7View Solutionવ્યતિકરણમાં ઊર્જા...
- 8View Solutionબિંદુવ્ત ઉદ્ગમ અને પડદા વચ્ચેનું અંતર બમણું કરતાં પડદા પર પ્રકાશની તીવ્રતા કેટલા ગણી થાય?
- 9$6000\,\mathring A$ તરંગલંબાઈ ધરાવતો પ્રકાશ સ્લિટ પર આપાત થાય. સ્લિટની પહોળાઈ $ 0.30 $ મીલીમીટર છે. સ્લિટથી $2$ મીટરના અંતરે પડદો આવેલ છે. પ્રથમ ન્યૂનત્તમ શલાકાનું સ્થાન શોધો.View Solution
- 10બે સ્લિટના પ્રયોગમાં બે સ્લિટો વચ્ચેનું અંતર $1 \;mm $ અને સ્લિટથી પડદા વચ્ચેનું અંતર $1 \;m$ છે. $500\;nm$ તરંગલંબાઇ ધરાવતા એકરંગી પ્રકાશનો ઉપયોગ કર્યો છે. બે સ્લિટ માટે દસમાં અધિકતમ જેટલું જ એક સ્લિટથી મધ્યસ્થ અધિકતમ મળે, તો દરેક સ્લિટની પહોળાઈ ($mm$ માં) કેટલી હશે?View Solution
