$T$ તાપમાને રહેલા ગોળાથી $d$ અંતરે મળતો પાવર $P$ છે.જો ગોળાનું તાપમાન અને અંતર બમણું કરતાં મળતો પાવર કેટલો હોય ?
Diffcult
b
(b) Energy received per second i.e., power \(P \propto ({T^4} - T_0^4)\)
(b) Energy received per second i.e., power \(P \propto ({T^4} - T_0^4)\)
==> \(P \propto {T^4}\) Also energy received per sec (p)\( \propto \frac{1}{{{d^2}}}\) (inverse square law)
==> \(P \propto \frac{{{T^4}}}{{{d^2}}}\)
==> \(\frac{{{P_1}}}{{{P_2}}} = {\left( {\frac{{{T_1}}}{{{T_2}}}} \right)^4} \times {\left( {\frac{{{d_2}}}{{{d_1}}}} \right)^2}\)
==> \(\frac{P}{{{P_2}}} = {\left( {\frac{T}{{2T}}} \right)^2} \times {\left( {\frac{{2d}}{d}} \right)^2} = \frac{1}{4}\) ==>\({P_2} = 4P.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક નળાકાર ધાતુનો સળિયો જેના બે છેડા બે ઉષ્મા સ્થાનો સાથે ઉષ્મિય સંપર્કમાં રાખતા તેમાંથી $t$ સમયમાં $Q$ ઉષ્મા પસાર થાય છે. આ સળિયાને પિગાળીને તેમાંથી મૂળ સળિયા કરતાં અડધી ત્રિજયાનો નવો સળિયો બનાવવામાં આવે છે. જ્યારે આ નવા સળિયાના છેડાને બે ઉષ્મા સ્થાનો સાથે ઉષ્મિય સંપર્કમાં રાખવામાં આવે, તો આ નવા સળિયા દ્વારા $t$ સમયમાં પસાર થતી ઉષ્મા કેટલી હશે?View Solution
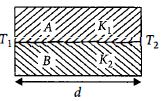
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે જુદા-જુદા દ્રવ્યમાંથી બનેલા બે સળિયા $A$ અને $B$ ને એકસાથે વેલ્ડ કરવામાં આવે છે. આ સળિયાઓની ઉષ્મા વાહકતા અનુક્રમે $K _{1}$ અને $K _{2}$ છે. બનેલા સંયુક્ત સળિયાની ઉષ્મા વાહકતા કેટલી થાય?View Solution
- 3$3000\,K$ તાપમાને રહેલ ફર્નેસ $1$ કલાકમાં એકમ ક્ષેત્રફળ દીઠ કેટલી ઉષ્મા વિકેરિત કરે? $( \sigma = 5. 7 \times 10^{-8}\,W\,m^{-2}\,K^{-4})$View Solution
- 4View Solutionન્યૂટનના કુલીંગના નિયમ પ્રમાણએ પદાર્થના કુલીંગનો દર ........ ના સમપ્રમાણમાં છે.
- 5$600\,K$ તાપમાને રહેલ ગોળાને $200\,K$ તાપમાનવાળા વાતાવરણમાં મુકેલ છે.તેનો ઠંડા પડવાનો દર $H$ છે.જો તેનું તાપમાન ઘટીને $400\,K$ થાય તો તેટલા જ વાતાવરણમાં તેનો ઠંડા પડવાનો દર કેટલો થાય?View Solution
- 6સમાન દ્રવ્ય અને સમાન દળ ધરાવતા ગોળો,સમઘન અને વર્તુળાકાર તકતીને $1000^°C$ તાપમાને ગરમ કરીને મૂકતાં કોણ વહેલું ઠંડું પડશે?View Solution
- 7${227^o}C$ તાપમાને રહેલ કાળો પદાર્થ $ 20\,W$ પાવરનું ઉત્સર્જન કરે છે.જો કાળા પદાર્થનું તાપમાન ${727^o}C$ થાય તો ..... $W$ પાવરનું ઉત્સર્જન કરશે?View Solution
- 8$0^°C$ તાપમાને રહેલ પદાર્થમાંથી ઉત્સર્જન પાવર $E \,J/sec$ છે,તો $ {273^o}C $ તાપમાને રહેલ તે જ પદાર્થનો ઉત્સર્જન પાવર કેટલો થાય?View Solution
- 9$25^{\circ} {C}$ તાપમાનવાળા ઓરડામાં $5\, minutes$ માં પદાર્થનું તાપમાન $75^{\circ} {C}$ થી $65^{\circ} {C}$ થાય છે. પછીની $5\, minutes$ માં પદાર્થનું તાપમાન (${ }^{\circ} {C}$ માં) કેટલું થાય?View Solution
- 10સ્લેબ સમાન જાડાઈના કોપર અને બ્રાસના બે સમાંતર સ્તર છે અને ઉષ્મીય વાહકતા $1:4$ ના ગુણોત્તર છે. જો બ્રાસની મુક્ત બાજુનું તાપમાન $100°C$ અને કોપરનું $0°C$ છે. તો અત:બાજુનું તાપમાન ....... $^oC$ છે.View Solution
