Given: \(f_{0}=50\, \mathrm{cm}, f_{e}=5\, \mathrm{cm}\)
\(\mathrm{d}=25\, \mathrm{cm}, \mathrm{u}_{0}=-200\, \mathrm{cm}\)
Magnification \(\mathrm{M}=?\)
As \(\frac{1}{\mathrm{v}_{0}}-\frac{1}{\mathrm{u}_{0}}=\frac{1}{\mathrm{f}_{0}}\)
\(\Rightarrow \frac{1}{v_{0}}=\frac{1}{f_{0}}+\frac{1}{u_{0}}=\frac{1}{50}-\frac{1}{200}=\frac{4-1}{200}=\frac{3}{200}\)
or \(\quad v_{0}=\frac{200}{3}\, \mathrm{cm}\)
Now \(v_{e}=d=-25\, \mathrm{cm}\)
From. \(\frac{1}{v_{e}}-\frac{1}{u_{e}}=\frac{1}{f_{c}}\)
\(-\frac{1}{u_{k}}=\frac{1}{f_{e}}-\frac{1}{v_{e}}\)
\(=\frac{1}{5}+\frac{1}{25}=\frac{6}{25}\)
or. \(\quad u_{e}=\frac{-25}{6}\, \mathrm{cm}\)
Magnification \(\mathrm{M}=\mathrm{M}_{0} \times \mathrm{M}_{\mathrm{e}}\)
\(=\frac{v_{0}}{u_{0}} \times \frac{v_{c}}{u_{e}}=\frac{-200 / 3}{200} \times \frac{-25}{-25 / 6}\)
\(=-\frac{1}{3} \times 6=-2\)
Download our appand get started for free
Similar Questions
- 1વક્રીભવનાંક વાળા પ્રિઝમ દ્વારા $\mu$ વિચલન પામે છે અને નાનો કોણ $A$ ને ............દ્વારા આપવામાં આવે છે.View Solution
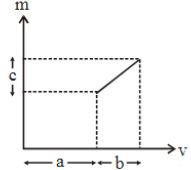
- 2પાતળા લેન્સ માટે મોટવણી $m$ વિરુદ્ધ પ્રતિબિંબ અંતર $v$ નો આલેખ આપેલ છે.તો લેન્સની કેન્દ્રલંબાઈ કેટલી હશે?View Solution
- 3ઓપ્ટીકલ ફાઈબરમાં અંદરના ભાગનો વક્રીભવનાંક $1.68$ અને બહારના ભાગનો વક્રીભવનાંક $1.44$ છે. ફાઈબરનું આકડાકીય મુખ કેટલું છે ?View Solution
- 4View Solutionકાંચમાંથી હવામાં પ્રકાશ પસાર થાય ત્યારે, લઘુત્તમ ક્રાંતિકોણ કયા કલરનો હોય છે?
- 5$6cm$ કેન્દ્રલંબાઇ ધરાવતા અંર્તગોળ અરીસાથી પ્રતિબિંબ વસ્તુ કરતાં $3$ ગણું મળે છે.તો વસ્તુ અંતર કેટલા ......$cm$ હશે?View Solution
- 6$20\,\, cm$ કેન્દ્રલંબાઈનો બહિર્ગોળ લેન્સ અને $f$ કેન્દ્રલંબાઈનો અંતર્ગોળ અરીસાને $5\,\, cm$ અંતરે સમઅક્ષીય રીતે જોડેલા છે. સમાંતર પ્રકાશનું પુંજ બહિર્ગોળ લેન્સ પર આપાત થઈને અંતર્ગોળ લેન્સમાંથી સમાંતર પુંજ સ્વરૂપે નિર્ગમન પામે છે. તો $f = ….cm$View Solution
- 7$P$ બિંદુ એ પ્રકાશ કિરણ પુંજ અભિકેન્દ્રીત થાય છે. $P$ બિંદુથી $12\,\, cm$ પ્રકાશ પુંજના પથ પર એક લેન્સ મૂકવામાં આવે છે. જો લેન્સ $16\,\, cm$ કેન્દ્રલંબાઈ ધરાવતો અંતર્ગોળ કાચ હોય, તો ક્યાં......$cm$ બિંદુએ કિરણપુંજ અભિકેન્દ્રિત થાય?View Solution
- 8બહિર્ગોળ લેન્સ વડે રચાતા વાસ્તવિક પ્રતિબિંબ અને વાસ્તવિક વસ્તુ વચ્ચેનું અંતર $56\, cm$ છે. તો લેન્સની કેન્દ્રલંબાઈ કેટલી છે.View Solution
- 9$f$ કેન્દ્રલંબાઈ ધરાવતા અંતગોળ લેન્સ માટે વસ્તુ અંતર $u$ અને પ્રતિબિંબ અંતર $v$ વચ્ચેનો આલેખ $( u = v$ સંદર્ભ રેખા)View Solution
- 10એક ટાંકી $12.5\,cm$ ઉંચાઈ સુધી પાણીથી ભરેલી છે. ટાંકીને નીચેની સપાટી પર પડેલી સોયની આભાસી ઉડાઈ માઈક્રોસ્કોપ વડે માપવામાં આવતાં $9.4\, cm$ મળે છે. જો તે જ ઉંચાઈ સુધી પાણીને $1.63$ વક્રીભવનાંક વાળા પાણીથી બદલવામાં આવે તો સોયની આભાસી ઉંડાઈ કેટલા ........$cm$ હશે?View Solution
